Comment une entreprise peut-elle utiliser solveur pour déterminer les projets qu’elle doit entreprendre ?
Chaque année, une entreprise comme Eli Lilly doit déterminer les médicaments à développer ; une société comme Microsoft, qui les logiciels à développer ; une société comme Proctor & Gamble, qui de nouveaux produits grand public à développer. La fonctionnalité Solveur dans Excel peut aider une entreprise à prendre ces décisions.
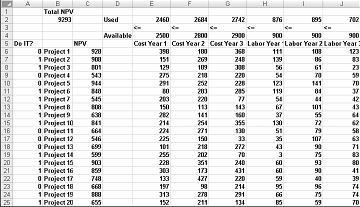
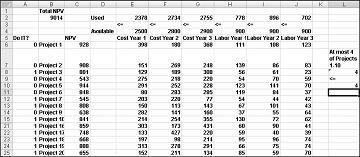
La plupart des entreprises veulent entreprendre des projets qui contribuent à la plus grande valeur actuelle nette (VNB), sous réserve de ressources limitées (généralement du capital et de la main-d’œuvre). Supposons qu’une société de développement de logiciels tente de déterminer lequel des 20 projets logiciels qu’elle doit entreprendre. La VALEUR NPV (en millions de dollars) de chaque projet ainsi que le capital (en millions de dollars) et le nombre de programmeurs nécessaires au cours de chacune des trois prochaines années sont indiqués dans la feuille de calcul Modèle de base dans le fichier Capbudget.xlsx, qui est illustré dans la figure 30-1 de la page suivante. Par exemple, le projet 2 génère 908 millions de dollars. Il a besoin de 151 millions de dollars au cours de la 1er année, de 269 millions de dollars pendant l’année 2 et de 248 millions de dollars au cours de l’année 3. Project 2 nécessite 139 programmeurs pendant l’année 1, 86 programmeurs pendant l’année 2 et 83 programmeurs pendant l’année 3. Les cellules E4 :G4 indiquent le capital (en millions de dollars) disponible au cours de chacune des trois années, et les cellules H4 :J4 indiquent le nombre de programmeurs disponibles. Par exemple, pendant l’année 1, jusqu’à 2,5 milliards de dollars en capital et 900 programmeurs sont disponibles.
L’entreprise doit décider si elle doit entreprendre chaque projet. Supposons que nous ne pouvons pas entreprendre une fraction d’un projet de logiciel ; si nous allouons 0,5 des ressources nécessaires, par exemple, nous aurions un programme sans travail qui nous apporterait 0 $ de revenus !
L’astuce dans la modélisation des situations dans lesquelles vous faites ou ne faites pas quelque chose consiste à utiliser des cellules binaires à changement. Une cellule à variation binaire est toujours égale à 0 ou 1. Lorsqu’une cellule à modification binaire qui correspond à un projet est égale à 1, nous effectuons le projet. Si une cellule binaire qui correspond à un projet est égale à 0, nous ne faisons pas le projet. Vous configurez solveur pour utiliser une plage de cellules binaires à modification en ajoutant une contrainte : sélectionnez les cellules modifiables que vous souhaitez utiliser, puis choisissez Bin dans la liste de la boîte de dialogue Ajouter une contrainte.
Avec cet arrière-plan, nous sommes prêts à résoudre le problème de sélection de projet logiciel. Comme toujours avec un modèle Solver, nous commençons par identifier notre cellule cible, les cellules changeantes et les contraintes.
-
Cellule cible. Nous optimisons la valeur NPV générée par les projets sélectionnés.
-
Modification des cellules. Nous recherchons une cellule à variation binaire 0 ou 1 pour chaque projet. J’ai localisé ces cellules dans la plage A6 :A25 (et j’ai nommé la plage doit). Par exemple, un 1 dans la cellule A6 indique que nous entreprenons le projet 1 ; un 0 dans la cellule C6 indique que nous n’entreprenons pas le projet 1.
-
Contraintes. Nous devons nous assurer que pour chaque année t (t=1, 2, 3), année t le capital utilisé est inférieur ou égal à l’année t capital disponible, et que l’année t travail utilisé est inférieur ou égal à l’année t travail disponible.
Comme vous pouvez le voir, notre feuille de calcul doit calculer pour toute sélection de projets la VAN, le capital utilisé annuellement et les programmeurs utilisés chaque année. Dans la cellule B2, j’utilise la formule SUMPRODUCT(doit,NPV) pour calculer la valeur NPV totale générée par les projets sélectionnés. (Le nom de plage NPV fait référence à la plage C6 :C25.) Pour chaque projet avec un 1 dans la colonne A, cette formule récupère la valeur NPV du projet, et pour chaque projet avec un 0 dans la colonne A, cette formule ne récupère pas la valeur NPV du projet. Par conséquent, nous sommes en mesure de calculer la valeur NPV de tous les projets, et notre cellule cible est linéaire, car elle est calculée en additionnant les termes qui suivent la forme (cellule changeante)*(constante). De la même façon, je calcule le capital utilisé chaque année et le travail utilisé chaque année en copiant de E2 vers F2 :J2 la formule SUMPRODUCT(doit,E6 :E25).
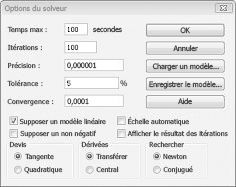
Je renseigne maintenant la boîte de dialogue Paramètres du solveur, comme illustré dans la figure 30-2.
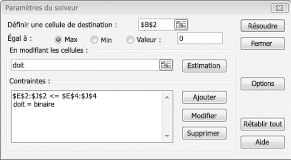
Notre objectif est d’optimiser la VAN des projets sélectionnés (cellule B2). Nos cellules changeantes (la plage nommée doit) sont les cellules binaires à variation pour chaque projet. La contrainte E2 :J2<=E4 :J4 garantit qu’au cours de chaque année le capital et la main-d’œuvre utilisés sont inférieurs ou égaux au capital et au travail disponibles. Pour ajouter la contrainte qui rend les cellules modifiables binaires, je clique sur Ajouter dans la boîte de dialogue Paramètres du solveur, puis je sélectionne Bin dans la liste au milieu de la boîte de dialogue. La boîte de dialogue Ajouter une contrainte doit apparaître comme indiqué dans la figure 30-3.
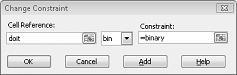
Notre modèle est linéaire, car la cellule cible est calculée comme la somme des termes qui ont la forme (cellule changeante)*(constante) et parce que les contraintes d’utilisation des ressources sont calculées en comparant la somme de (cellules changeantes)*(constantes) à une constante.
Une fois la boîte de dialogue Paramètres du solveur renseignée, cliquez sur Résoudre pour obtenir les résultats présentés plus haut dans la Figure 30-1. L’entreprise peut obtenir une valeur NPV maximale de 9 293 millions de dollars (9,293 milliards de dollars) en choisissant Les projets 2, 3, 6 à 10, 14 à 16, 19 et 20.
Parfois, les modèles de sélection de projet ont d’autres contraintes. Par exemple, supposons que si nous sélectionnons Project 3, nous devons également sélectionner Project 4. Étant donné que notre solution optimale actuelle sélectionne Project 3 mais pas Project 4, nous savons que notre solution actuelle ne peut pas rester optimale. Pour résoudre ce problème, ajoutez simplement la contrainte selon laquelle la cellule de modification binaire pour Project 3 est inférieure ou égale à la cellule de modification binaire pour Project 4.
Vous trouverez cet exemple dans la feuille de calcul Si 3 puis 4 dans le fichier Capbudget.xlsx, qui est illustré dans la figure 30-4. La cellule L9 fait référence à la valeur binaire liée au projet 3 et la cellule L12 à la valeur binaire liée au projet 4. En ajoutant la contrainte L9<=L12, si nous choisissons Project 3, L9 est égal à 1 et notre contrainte force L12 (le binaire project 4) à égal à 1. Notre contrainte doit également laisser la valeur binaire dans la cellule de modification de Project 4 illimitée si nous ne sélectionnons pas Project 3. Si nous ne sélectionnons pas Project 3, L9 est égal à 0 et notre contrainte permet au binaire Project 4 d’être égal à 0 ou 1, ce que nous voulons. La nouvelle solution optimale est illustrée dans la figure 30-4.
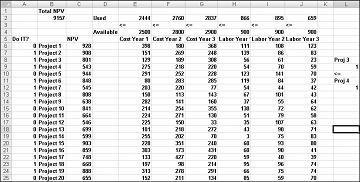
Une nouvelle solution optimale est calculée si la sélection du projet 3 signifie que nous devons également sélectionner Project 4. Supposons maintenant que nous ne pouvons réaliser que quatre projets parmi les projets 1 à 10. (Voir la feuille de calcul Au maximum 4 de P1-P10 , illustrée dans la figure 30-5.) Dans la cellule L8, nous calculons la somme des valeurs binaires associées aux projets 1 à 10 avec la formule SOMME(A6 :A15). Ensuite, nous ajoutons la contrainte L8<=L10, ce qui garantit que, au maximum, 4 des 10 premiers projets sont sélectionnés. La nouvelle solution optimale est illustrée dans la figure 30-5. La VAN a chuté à 9,014 milliards de dollars.
Les modèles solveurs linéaires dans lesquels une partie ou la totalité des cellules à variation doivent être binaires ou entières sont généralement plus difficiles à résoudre que les modèles linéaires dans lesquels toutes les cellules changeantes sont autorisées à être des fractions. Pour cette raison, nous sommes souvent satisfaits d’une solution quasi optimale à un problème de programmation binaire ou entier. Si votre modèle solveur s’exécute pendant une longue période, vous pouvez envisager d’ajuster le paramètre Tolérance dans la boîte de dialogue Options du solveur. (Voir figure 30-6.) Par exemple, un paramètre tolérance de 0,5 % signifie que le solveur s’arrête la première fois qu’il trouve une solution réalisable qui se trouve à moins de 0,5 % de la valeur théorique optimale de la cellule cible (la valeur théorique optimale de la cellule cible est la valeur cible optimale trouvée lorsque les contraintes binaires et entières sont omises). Souvent, nous sommes confrontés à un choix entre trouver une réponse dans un délai de 10 pour cent d’optimal en 10 minutes ou trouver une solution optimale dans deux semaines de temps d’ordinateur ! La valeur de tolérance par défaut est 0,05 %, ce qui signifie que le solveur s’arrête lorsqu’il trouve une valeur de cellule cible comprise dans 0,05 % de la valeur théorique optimale de la cellule cible.
-
Une entreprise a neuf projets à l’étude. Le NPV ajouté par chaque projet et le capital requis par chaque projet au cours des deux prochaines années sont indiqués dans le tableau suivant. (Tous les nombres sont en millions.) Par exemple, le projet 1 ajoutera 14 millions de dollars en VAN et exigera des dépenses de 12 millions de dollars au cours de l’année 1 et de 3 millions de dollars au cours de l’année 2. Au cours de l’année 1, 50 millions de dollars en capital sont disponibles pour les projets, et 20 millions de dollars au cours de l’année 2.
|
VAN |
Dépenses de l’année 1 |
Dépenses de l’année 2 |
|
|---|---|---|---|
|
Projet 1 |
14 |
12 |
3 |
|
Projet 2 |
17 |
54 |
7 |
|
Projet 3 |
17 |
6 |
6 |
|
Projet 4 |
15 |
6 |
2 |
|
Projet 5 |
40 |
30 |
35 |
|
Projet 6 |
12 |
6 |
6 |
|
Projet 7 |
14 |
48 |
4 |
|
Projet 8 |
10 |
36 |
3 |
|
Projet 9 |
12 |
18 |
3 |
-
Si nous ne pouvons pas entreprendre une fraction d’un projet, mais que nous devons entreprendre la totalité ou l’absence d’un projet, comment pouvons-nous maximiser la VAN ?
-
Supposons que si le projet 4 est entrepris, le projet 5 doit l’être. Comment pouvons-nous optimiser la van de la valeur réseau ?
-
Une société d’édition tente de déterminer lequel des 36 livres qu’elle devrait publier cette année. Le fichier Pressdata.xlsx fournit les informations suivantes sur chaque livre :
-
Revenus et coûts de développement prévus (en milliers de dollars)
-
Pages de chaque livre
-
Si le livre est destiné à un public de développeurs de logiciels (indiqué par un 1 dans la colonne E)
Une société d’édition peut publier jusqu’à 8500 pages cette année et doit publier au moins quatre livres destinés aux développeurs de logiciels. Comment l’entreprise peut-elle maximiser ses bénéfices ?
-
Cet article a été adapté de Microsoft Office Excel 2007 Data Analysis and Business Modeling par Wayne L. Winston.
Ce livre de style de classe a été développé à partir d’une série de présentations de Wayne Winston, un statisticien et professeur de commerce bien connu qui se spécialise dans les applications créatives et pratiques d’Excel.










