Returns the cumulative lognormal distribution of x, where ln(x) is normally distributed with the parameters mean and standard_dev. Use this function to analyze data that has been logarithmically transformed.
Syntax
LOGNORMDIST(x,mean,standard_dev)
x is the value at which to evaluate the function.
Mean is the mean of ln(x).
Standard_dev is the standard deviation of ln(x).
Remarks
-
If any argument is nonnumeric, LOGNORMDIST returns the #VALUE! error value.
-
If x ≤ 0 or if standard_dev ≤ 0, LOGNORMDIST returns the #NUM! error value.
-
The equation for the lognormal cumulative distribution function is:
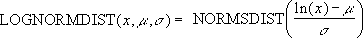
Example
|
X |
Mean |
StdDev |
Formula |
Description (Result) |
|
4 |
3.5 |
1.2 |
=LOGNORMDIST([X],[Mean],[StdDev]) |
Cumulative lognormal distribution at 4 with the specified arguments (0.039084) |










