Returns the hypergeometric distribution. HYPGEOMDIST returns the probability of a given number of sample successes, given the sample size, population successes, and population size. Use HYPGEOMDIST for problems with a finite population, where each observation is either a success or a failure, and where each subset of a given size is chosen with equal likelihood.
Syntax
HYPGEOMDIST(sample_s,number_sample,population_s,number_population)
Sample_s is the number of successes in the sample.
Number_sample is the size of the sample.
Population_s is the number of successes in the population.
Number_population is the population size.
Remarks
-
All arguments are truncated to integers.
-
If any argument is nonnumeric, HYPGEOMDIST returns the #VALUE! error value.
-
If sample_s < 0 or sample_s is greater than the lesser of number_sample or population_s, HYPGEOMDIST returns the #NUM! error value.
-
If sample_s is less than the larger of 0 or (number_sample - number_population + population_s), HYPGEOMDIST returns the #NUM! error value.
-
If number_sample < 0 or number_sample > number_population, HYPGEOMDIST returns the #NUM! error value.
-
If population_s < 0 or population_s > number_population, HYPGEOMDIST returns the #NUM! error value.
-
If number_population < 0, HYPGEOMDIST returns the #NUM! error value.
-
The equation for the hypergeometric distribution is:
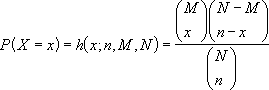
where:
x = sample_s
n = number_sample
M = population_s
N = number_population
HYPGEOMDIST is used in sampling without replacement from a finite population.
Example
A sampler of chocolates contains 20 pieces. Eight pieces are caramels, and the remaining 12 are nuts. If a person selects 4 pieces at random, the following function returns the probability that exactly 1 piece is a caramel.
|
Sample_s |
Number_sample |
Population_s |
Number_Population |
Formula |
Description (Result) |
|
1 |
4 |
8 |
20 |
=HYPGEOMDIST([Sample_s],[Number_sample],[Population_s],[Number_Population]) |
Hypergeometric distribution for sample and population (0.363261) |










