Huomautus: Microsoft haluaa tarjota sinulle ajantasaisinta ohjesisältöä mahdollisimman nopeasti omalla kielelläsi. Tämä sivu on käännetty automaation avulla, ja siinä saattaa olla kielioppivirheitä tai epätarkkuuksia. Tarkoitus on, että sisällöstä on sinulle hyötyä. Kertoisitko sivun alareunassa olevan toiminnon avulla, oliko tiedoista hyötyä? Tästä pääset helposti artikkelin englanninkieliseen versioon.
Tässä artikkelissa kerrotaan, miten Ratkaisin on Microsoft Excel-apuohjelma, jota voit käyttää Entä jos-analyyseissä optimaalisen tuote valikoiman määrittämiseen.
Miten voin arvioida kuukausittaista tuote valikoimaa, joka maksimoi kannattavuuden?
Yritysten on usein määritettävä kunkin tuotteen määrä kuukausittain. Yksinkertaisimmassa muodossaan tuote yhdistelmä ongelma on se, miten voit määrittää kunkin kuukauden aikana tuotetun tuotteen määrän voittojen maksimoimiseksi. Tuote valikoiman on yleensä noudatettava seuraavia rajoituksia:
-
Tuote valikoima ei voi käyttää enempää resursseja kuin käytettävissä.
-
Kunkin tuotteen kysyntä on rajoitettu. Emme voi tuottaa enemmän tuotetta kuukauden aikana kuin kysyntä sanelee, koska ylijäämä tuotanto menee hukkaan (esimerkiksi pilaantuva lääke).
Ratkaiskaamme nyt seuraava esimerkki tuote yhdistelmä ongelmasta. Ongelman ratkaisu löytyy tiedostosta Prodmix. xlsx, joka näkyy kuvassa 27-1.
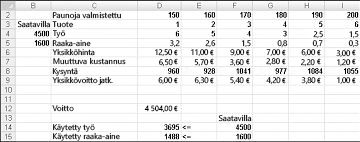
Oletetaan, että työskentelemme lääke yrityksessä, joka tuottaa kuusi eri tuotetta tehtaansa. Kunkin tuotteen tuotannossa tarvitaan työvoimaa ja raaka-aineita. Kuvassa 27-1 oleva rivi 4 ilmaisee työtunnit, jotka tarvitaan kunkin tuotteen punnan tuottamiseen, ja rivillä 5 on kiloja raaka-aineita, jotka tarvitaan kunkin tuotteen punnan tuottamiseen. Esimerkiksi tuote 1: n punnan tuottaminen vaatii kuusi työtuntia ja 3,2 kiloa raaka-ainetta. Kunkin lääkkeen hinta kiloa kohden annetaan rivillä 6, yksikkö hinta kiloa kohden annetaan riville 7 ja voitto-osuus kiloa kohden annetaan rivillä 9. Esimerkiksi tuote 2 myy $11,00 kiloa kohden, ja sen yksikkö hinta on $5,70 puntaa kohden, ja se antaa lisää tuottoa kiloa kohden. Kuukauden vaatimus kullekin huumelle annetaan rivillä 8. Esimerkiksi tuotteen 3 kysyntä on 1041 kiloa. Tässä kuussa 4500 työtunnit ja 1600 kiloa raaka-ainetta on saatavilla. Miten tämä yritys voi suurentaa kuukausi tuottoa?
Jos emme tienneet mitään Excel-Ratkaisimesta, tätä ongelmaa voidaan hyökätä luomalla laskenta taulukko, jossa seurataan tuote yhdistelmään liittyvää voittoa ja resurssien käyttöä. Sen jälkeen käyttäisimme tuotetta ja virhettä, jos haluat muuttaa tuote valikoimaa ja optimoida voiton käyttämättä enemmän työvoimaa tai raaka-aineita kuin on saatavilla, ja tuottamatta mitään lääkkeitä liikaa kysyntää. Tässä prosessissa käytetään ratkaisinta vain koekäyttö-ja-virhe vaiheessa. Ratkaisin on pohjimmiltaan optimointi ohjelma, joka suorittaa virheettömästi haku-ja virhe haun.
Tuote yhdistelmä ongelman ratkaisemiseksi on tärkeää laskea tehokkaasti tiettyyn tuote yhdistelmään liittyvää resurssien käyttöä ja tuottoa. Tärkeä työkalu, jonka avulla voit tehdä tämän laskennan, on summa. tulo-funktio. Summa. Jos-funktio kertoo solu alueiden vastaavat arvot ja palauttaa kyseisten arvojen summan. Kullakin summa-arvon arvioinnissa käytetyillä solu alueella on oltava samat dimensiot, mikä tarkoittaa, että voit käyttää summa-tuotetta, jossa on kaksi riviä tai kaksi saraketta, mutta ei yhtä saraketta ja yhtä riviä.
Esimerkki siitä, miten voimme käyttää tuote valikoimme summa. Jos-funktiota, yritetään laskea resurssi käyttömme mukaan. Työn tekijöiden käyttö lasketaan
(Työvoima, jota käytetään huume kiloa kohden) * (huume 1 kiloa tuotettu) + (työvoima kiloa huumeita kohden 2) * (Drug 2 kiloa tuotettu) +... (Työvoimaa käytetty kiloa huumeita kohden 6) * (Drug 6 kiloa tuotettu)
Voisimme laskea työvoiman käytön entistä tylsäksi, kuten D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + i2 * I4. Vastaavasti raaka-aineiden käyttö voitiin laskea D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + i2 * i5. Näiden kaavojen syöttäminen kuuden tuotteen laskenta taulukkoon on kuitenkin aikaavievää. Kuvittele, kuinka kauan kestää, jos työskentelet yrityksessä, joka tuotti esimerkiksi 50-tuotteita tehtaansa. Paljon helpompi työn ja raaka-aineiden käyttö on kopioida D14-D15 kaavan SUMMA-funktion kautta ($D $2: $I $2, D4: i4). Tämä kaava laskee D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + i2 * I4 (joka on meidän työvoiman käyttö), mutta on paljon helpompi kirjoittaa! Huomaa, että käytän $-merkkiä, jonka arvo on D2: i2 niin, että kun kopioin kaavan, tallentan edelleen tuote valikoiman riviltä 2. Solun D15 kaava laskee raaka-aine käytön.
Vastaavalla tavalla, voitto määräytyy
(Drug 1 voitto per punta) * (huume 1 kiloa tuotettu) + (huume 2 voitto per punta) * (Drug 2 kiloa tuotettu) +... (Drug 6 voitto per punta) * (Drug 6 kiloa tuotettu)
Voitto on helppo laskea soluun D12 kaavan SUMMA-funktion avulla (D9: i9, $D $2: $I $2).
Nyt voimme tunnistaa tuote valikoiman Ratkaisimen kolme komponenttia.
-
Kohde solu.Tavoitteen amme on voittojen maksimoinnin (laskettu soluun D12).
-
Solujen vaihtamista.Kunkin tuotteen tuottamien puntien määrä (lueteltu solu alueella D2: i2)
-
Rajoitukset. Meillä on seuraavat rajoitukset:
-
Älä käytä enemmän työvoimaa tai raaka-aineita kuin on saatavilla. Solujen D14: D15 (Käytetyt resurssit) arvojen on oltava pienemmät tai yhtä suuret kuin solut F14: F15 (käytettävissä olevat resurssit).
-
Älä tuota enempää lääkettä kuin on kysyntää. Toisin kuin soluissa D2: i2 (kunkin huumeen tuotettu) on oltava pienempi tai yhtä suuri kuin kunkin huumeen (lueteltu soluissa B2:d: I8).
-
Emme voi tuottaa negatiivista määrää mitään huumeita.
-
Näytän, miten voit määrittää kohde solun, muuttuvat solut ja rajoitukset Ratkaisin. Sinun tarvitsee vain klikata ratkaise-painiketta ja etsiä voiton maksimoinnin tuote valikoima.
Aloita valitsemalla tiedot-väli lehti ja valitsemalla analysointi-ryhmästä Ratkaisin.
Huomautus: Kuten luvussa 26, "esittely: optimointi Excel-Ratkaisimen avulla", Ratkaisin asennetaan napsauttamalla Microsoft Office-painiketta ja valitsemalla sitten Excelin asetukset ja apuohjelmat. Valitse hallinta-luettelosta Excel-apuohjelmat, tarkista Ratkaisin-apuohjelma-valinta ruutu ja valitse sitten OK.
Ratkaisimen parametrit-valinta ikkuna tulee näkyviin, kuten kuvassa 27-2.
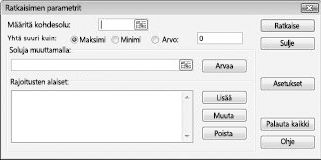
Napsauta Määritä kohde-solu-ruutua ja valitse sitten voitto soluksi (solu D12). Napsauta muuta soluja-ruutua ja osoita sitten Range D2: i2, joka sisältää jokaisesta lääkkeestä tuotettua kiloa. Valinta ikkunassa pitäisi nyt näkyä kuva 27-3.
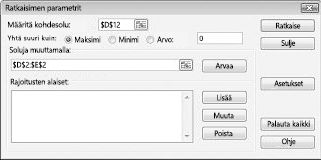
Olemme nyt valmiita lisäämään malliin rajoitteita. Napsauta Lisää-painiketta. Näkyviin tulee lisää rajoitus-valinta ikkuna, joka on kuvassa 27-4.
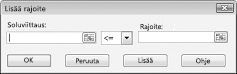
Jos haluat lisätä resurssien käyttö rajoitukset, napsauta solu viittaus-ruutua ja valitse sitten D14: D15. Valitse < = Keski luettelosta. Napsauta rajoite-ruutua ja valitse solu alueet F14: F15. Lisää rajoitus-valinta ikkunan pitäisi nyt näyttää kuvassa 27-5.
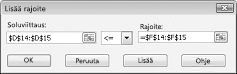
Olemme nyt varmistaneet, että kun Ratkaisin yrittää muuttaa solujen arvoja, vain ne yhdistelmät, jotka täyttävät molemmat D14< = F14 (käytetty työmäärä on pienempi tai yhtä suuri kuin työn tekijöiden käytettävissä) ja D15< = F15 (käytetty raaka-aine on pienempi tai yhtä suuri kuin saatavilla oleva raaka-aine) otetaan huomioon. Lisää kysynnän rajoitukset valitsemalla Lisää. Täytä lisää rajoite-valinta ruutu kuvan 27-6 mukaisesti.
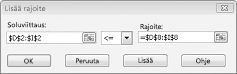
Näiden rajoitusten lisääminen varmistaa, että kun Ratkaisin yrittää eri yhdistelmiä muuttuvien solujen arvojen osalta, vain seuraavia parametreja vastaavat yhdistelmät otetaan huomioon:
-
D2< = B2:d (huume määrä 1 on pienempi tai yhtä suuri kuin huumeiden kysyntä 1)
-
E2< = E8 (huume määrä 2 on pienempi tai yhtä suuri kuin huumaus aineiden kysyntä 2)
-
F2< = F8 (huumeiden tuottama 3-arvo on pienempi tai yhtä suuri kuin huumaus aineiden kysyntä 3)
-
G2< = G8 (huume määrän 4 tuottama summa on pienempi tai yhtä suuri kuin huumeiden kysyntä 4)
-
H2< = H8 (lääkkeiden 5 tuottama summa on pienempi tai yhtä suuri kuin huumaus aineiden kysyntä 5)
-
I2< = I8 (lääkkeiden 6 tuottama määrä on pienempi tai yhtä suuri kuin huumaus aineiden kysyntä 6)
Valitse Lisää rajoitus-valinta ikkunassa OK. Ratkaisin-ikkunan pitäisi näyttää kuvassa 27-7.
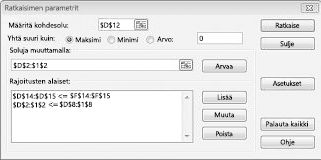
Lisää rajoitus, jonka mukaan solujen vaihtamisen on oltava ei-negatiivinen Ratkaisimen asetukset-valinta ikkunassa. Napsauta Ratkaisimen parametrit-valinta ikkunan asetukset-painiketta. Valitse oletetaan lineaarinen malli-ruutu ja oleta ei-negatiivinen-ruutu seuraavan sivun kuvassa 27-8. Valitse OK.
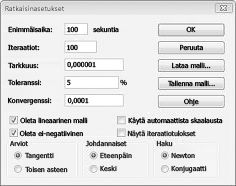
Jos oletetaan, että ei-negatiivinen-ruutu on olemassa, Ratkaisin ottaa huomioon vain sellaisten solujen yhdistelmät, joissa jokainen muuttuva solu olettaa ei-negatiivisen arvon. Olemme tarkastaneet oletetaan lineaarinen malli-ruudun, koska tuote valikoima ongelma on erityinen Ratkaisimen ongelma eli lineaarinen malli. Ratkaisimen malli on periaatteessa lineaarinen seuraavissa olosuhteissa:
-
Kohde solu lasketaan laskemalla yhteen lomakkeen ehdot (muuttuvat solut) * (vakio).
-
Jokainen rajoitus täyttää "lineaarisen malli vaatimuksen". Tämä tarkoittaa, että kukin rajoite lasketaan laskemalla yhteen lomakkeen ehdot (muuttuvat solut) * (vakio) ja vertaamalla summia vakioksi.
Miksi tämä Ratkaisin ongelma on lineaarinen? Kohde soluksi (voitto) lasketaan
(Drug 1 voitto per punta) * (huume 1 kiloa tuotettu) + (huume 2 voitto per punta) * (Drug 2 kiloa tuotettu) +... (Drug 6 voitto per punta) * (Drug 6 kiloa tuotettu)
Tämä laskenta noudattaa kaavaa, jossa kohde solun arvo johdetaan laskemalla yhteen lomakkeen ehdot (muuttuvat solut) * (vakio).
Työn tekijöiden rajoitus on laskettu vertaamalla (työvoimaa käytetään huume kiloa kohden 1) * (huume 1 naulaa tuotettu) + (työvoima kiloa kohden huumeita 2) * (huume 2 kiloa tuotettu) +... (Labour USEd/kiloa huumeita 6) * (Drug 6 kiloa tuotettu) työvoiman saatavilla.
Tämän vuoksi työrajoitus lasketaan laskemalla yhteen lomakkeen ehdot (muuttuvat solut) * (vakio) ja vertaamalla summia vakioksi. Sekä työvoiman rajoitus että raaka-aine rajoitus täyttävät lineaarisen malli vaatimuksen.
Vaatimuksemme rajoitukset ovat muotoa
(Drug 1 tuotettu) _LT_ = (Drug 1 demand) (huume 2 tuotettu) _LT_ = (Drug 2 demand) § (huume 6 tuotettu) _LT_ = (Drug 6 demand)
Jokainen vaatimus rajoitus täyttää myös lineaarisen malli vaatimuksen, koska kukin niistä lasketaan laskemalla yhteen lomakkeen ehdot (muuttuvat solut) * (vakio) ja vertaamalla summia vakioksi.
Miksi meidän pitäisi huolehtia siitä, että tuote valikoima mallimme on lineaarinen malli?
-
Jos Ratkaisimen malli on lineaarinen ja valitset oletetaan lineaarinen malli-vaihto ehdon, Ratkaisin on Taatusti löytänyt optimaalisen ratkaisun Ratkaisimen malliin. Jos Ratkaisimen malli ei ole lineaarinen, Ratkaisin ei ehkä löydä optimaalista ratkaisua.
-
Jos Ratkaisimen malli on lineaarinen ja valitset oletetaan lineaarinen malli, Ratkaisin käyttää erittäin tehokasta algoritmia (yksipuolinen menetelmä), jonka avulla voit löytää mallin optimaalisen ratkaisun. Jos Ratkaisimen malli on lineaarinen eikä Valitse oleta lineaarinen malli, Ratkaisin käyttää erittäin tehotonta algoritmia (GRG2 menetelmä), ja sen on ehkä vaikea löytää mallin optimaalista ratkaisua.
Kun valitset Ratkaisimen asetukset-valinta ikkunassa OK, palataan pääratkaisin-valinta ikkunaan, joka näkyy kuvassa 27-7. Kun valitset ratkaise, Ratkaisin laskee tuote valikoima mallimme optimaalisen ratkaisun (jos sellainen on olemassa). Kuten totesin luvussa 26, optimaalinen ratkaisu tuote valikoima malli olisi joukko muuttuvat solujen arvot (naulaa tuotetaan kunkin lääkkeen), joka maksimoi voiton joukko kaikkia toteuttamiskelpoisia ratkaisuja. Taas toteuttamiskelpoinen ratkaisu on joukko muuttuvien solujen arvoja, jotka täyttävät kaikki rajoitukset. Kuviossa 27-9 näkyvät solujen arvon muutokset ovat toteuttamiskelpoisia ratkaisuja, koska kaikki tuotanto tasot eivät ole negatiivisia, tuotanto tasot eivät ylitä kysyntää ja resurssien käyttö ei ylitä käytettävissä olevia resursseja.
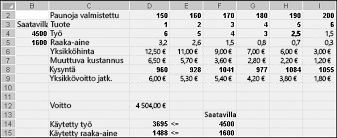
Seuraavan sivun kuvassa 27-10 olevat muuttuvat solu arvot ovat toteuttamiskelpoisia ratkaisuja seuraavista syistä:
-
Tuotamme enemmän huumeita 5 kuin sen kysyntää.
-
Käytämme enemmän työvoimaa kuin mitä on saatavilla.
-
Käytämme enemmän raaka-aineita kuin mitä on saatavilla.
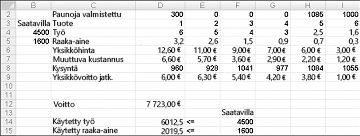
Kun olet napsauttanut ratkaise, Ratkaisin löytää nopeasti optimaalisen ratkaisun, joka näkyy kuvassa 27-11. Sinun on valittava Säilytä Ratkaisimen ratkaisu, jos haluat säilyttää laskenta taulukon optimaalisten ratkaisujen arvot.
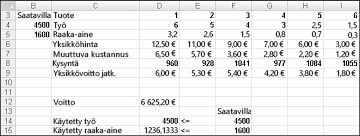
Huume yrityksemme voi suurentaa kuukausi tuottoa $6 625,20 tuottamalla 596,67 kiloa huumeita 4, 1084 kiloa huumeita 5, eikä yksikään muu huume! Emme voi määrit, onnistuuko $6 625,20 maksimi voitto muilla tavoilla. Voimme olla varmoja siitä, että rajallisia resurssejamme ja vaatimuksemme ansiosta ei ole mahdollista tehdä enempää kuin $6 627,20 tässä kuussa.
Oletetaan, että kunkin tuotteen kysynnän on täytyttävä. (Katso ei toteuttamiskelpoista ratkaisu -laskenta taulukkoa tiedostosta prodmix. xlsx.) Sen jälkeen meidän on muutettava vaatimus rajojamme D2: I2< = B2:d: I8 – D2: I2> = B2:d: I8. Voit tehdä tämän avaamalla Ratkaisin, valitsemalla D2: I2< = B2:d: I8 rajoitus ja valitsemalla sitten muuta. Näkyviin tulee Muokkaa rajoitetta-valinta ikkuna, joka näkyy kuvassa 27-12.
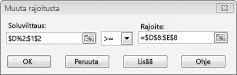
Valitse _T_ = ja valitse sitten OK. Nyt on varmistettu, että Ratkaisin harkitsee vain niiden solujen arvojen vaihtamista, jotka täyttävät kaikki vaatimukset. Kun valitset ratkaise, näyttöön tulee sanoma, jonka mukaan Ratkaisin ei löytänyt toteuttamiskelpoista ratkaisua. Tämä viesti ei tarkoita, että olisimme tehneet virheen malleistamme, vaan sen sijaan, että meillä olisi rajoitetut resurssit, emme voi täyttää kaikkien tuotteiden kysyntää. Ratkaisin kertoo meille vain, että jos halu amme täyttää kunkin tuotteen kysynnän, meidän on lisättävä enemmän työvoimaa, enemmän raaka-aineita tai enemmän molempia.
Katsotaan, mitä tapahtuu, jos sallimme kunkin tuotteen rajoittamattoman kysynnän ja sallimme kunkin lääkkeen negatiivisten määrien tuotannon. (Voit tarkastella tätä Ratkaisimen ongelmaa määrittämällä arvot eivät ole lähentyvät laskenta taulukkoa tiedostoon prodmix. xlsx.) Jos haluat löytää optimaalisen ratkaisun tähän tilanteeseen, avaa Ratkaisin, napsauta Asetukset-painiketta ja poista oleta ei-negatiivinen-valinta ruudun valinta. Valitse Ratkaisimen parametrit-valinta ikkunassa vaatimus rajoitus D2: I2< = B2:d: I8 ja valitse sitten Poista, jos haluat poistaa rajoituksen. Kun valitset ratkaise, Ratkaisin palauttaa viestin "solun arvojen asettaminen ei Lähennytä." Tämä viesti tarkoittaa, että jos kohde solu on tarkoitus maksimoida (kuten esimerkissä), on olemassa toteuttamiskelpoisia ratkaisuja, joilla on mielivaltaisesti suuria kohde solu arvoja. (Jos kohde solu on pienennettävä, viesti "solujen arvojen asettaminen ei ole yhteneviä" tarkoittaa, että on olemassa toteuttamiskelpoisia ratkaisuja, joilla on mielivaltaisesti pieniä kohde solu arvoja.) Tilanteessa, jossa lääkkeen negatiivinen tuotanto on käytössä, olemme itse asiassa "luoda" resursseja, joilla voidaan tuottaa mielivaltaisesti suuria määriä muita huumeita. Koska olemme rajoittamattomat, tämä antaa meille mahdollisuuden tehdä rajattomasti voittoja. Todellinen tilanne ei voi olla ääretön raha summa. Lyhyesti sanottuna, jos näet "arvojen asettaminen ei lähentyä", mallissa on virhe.
-
Oletetaan, että huume yrityksemme voi ostaa jopa 500 työtuntia $1 enemmän tunnissa kuin nykyiset työvoima kustannukset. Miten voimme hyötyä voiton maksimoinnin?
-
Siru tuotanto laitoksessa neljä teknikkoa (A, B, C ja D) tuottavat kolme tuotetta (tuotteet 1, 2 ja 3). Tässä kuussa siru valmistaja voi myydä 80 yksikköä tuotteen 1, 50 yksikköä tuotteesta 2 ja enintään 50 yksikköä tuotetta 3. Teknikko A voi tehdä vain tuotteita 1 ja 3. Teknikko B voi tehdä vain tuotteita 1 ja 2. Teknikko C voi tehdä vain tuotteen 3. Teknikko D voi tehdä vain tuotteen 2. Jokaisesta tuotetusta yksiköstä tuotteet tuottavat seuraavan tuoton: tuote 1; $6; Tuote 2, $7; ja tuote 3, $10. Aika (tunteina), jonka kukin teknikko tarvitsee tuotteen valmistamiseen, on seuraava:
Tuote
Teknikko A
Teknikko B
Teknikko C
Teknikko D
1
2
2,5
Ei voi tehdä
Ei voi tehdä
2
Ei voi tehdä
3
Ei voi tehdä
3,5
3
3
Ei voi tehdä
4
Ei voi tehdä
-
Jokainen teknikko voi työskennellä enintään 120 tuntia kuukaudessa. Miten siru valmistaja voi suurentaa kuukausi tuottoa? Oletetaan, että yksikköä voidaan tuottaa murto-osa.
-
Tieto koneen tuotanto laitos valmistaa hiiriä, näppäimistöjä ja video peli ohjaimia. Yksikkökohtainen tuotto, yksikkökohtainen Työkäyttö, kuukausittainen kysyntä ja yksikkökohtainen kone ajan käyttö on esitetty seuraavassa taulukossa:
Hiiret
Näppäimistöt
Peli ohjaimet
Voitto/yksikkö
$8
$11
$9
Työvoiman käyttö/yksikkö
.2 tuntia
.3 tuntia
.24 tuntia
Koneen aika/yksikkö
.04 tuntia
.055 tunti
.04 tuntia
Kuukausittainen kysyntä
15 000
27 000
11 000
-
Saatavilla on kuukausittain yhteensä 13 000 työtuntia ja 3000 tuntia koneen aikaa. Miten valmistaja voi suurentaa kuukausittain tuottoa tehtaasta?
-
Selvitä huume esimerkki olettaen, että 200-yksikön vähimmäisvaatimus kullekin huumelle on täytettävä.
-
Jason tekee timantti rannekkeita, kaula koruja ja korva koruja. Hän haluaa työskennellä enintään 160 tuntia kuukaudessa. Hän on 800 unssia timantteja. Kunkin tuotteen tuotannossa tarvittava tulos, työn aika ja unssia on esitetty alla. Jos kunkin tuotteen kysyntä on rajoittamaton, miten Jason voi suurentaa voittojensa tuottoa?
Tuote
Yksikön voitto
Työtunnit yksikköä kohden
Ruutu unssia yksikköä kohden
Ranne koru
300 €
.35
1,2
Kaula koru
200 €
.15
.75
Korva korut
100 €
.05
5










