ODDFPRICE function

Kuvaus

Palauttaa arvopaperin hinnan tilanteessa, jossa ensimmäinen kausi on normaalista poikkeava.

Syntaksi

PARITON.ENS.NIMELLISARVO(tilityspvm; erääntymispvm; asettamispvm; ens_korko; korko; tuotto; lunastushinta; korkojakso; [peruste])

PARITON.ENS.NIMELLISARVO-funktion syntaksissa on seuraavat argumentit:

• Tilityspvm    Pakollinen. Arvopaperin tilityspäivämäärä. Tilityspäivämäärä on se liikkeellelaskemispäivän jälkeinen päivämäärä, jolloin arvopaperi myydään ostajalle.

• Erääntymispvm    Pakollinen. Arvopaperin erääntymispäivä. Erääntymispäivä on päivä, jolloin arvopaperi vanhentuu.

• Ongelma    Pakollinen. Arvopaperin liikkeellelaskupäivämäärä.

• Ens_korko    Pakollinen. Arvopaperin ensimmäinen koronmaksupäivä.

• Korko Pakollinen. Arvopaperin korkoprosentti.

• Tuotto    Pakollinen. Arvopaperin vuosittainen tuotto.

• Lunastushinta    Pakollinen. Arvopaperin lunastushinta 100 euron nimellisarvoa vastaan.

• Korkojakso    Pakollinen. Nimelliskoron maksupäivien määrä vuodessa. Jos nimelliskorko maksetaan vuosittain, korkojakso on 1, jos maksetaan puolivuosittain, korkojakso on 2, ja jos se maksetaan neljännesvuosittain, korkojakso on 4.

• Peruste    Valinnainen. Päivien määrän laskentaperuste.

Huomautuksia

• Microsoft Excel tallentaa päivämäärät järjestyslukuina, jotta niitä voidaan käyttää laskennassa. Oletusarvoisesti päivämäärän 1.1.1900 järjestysluku on 1 ja päivämäärän 1.1.2008 järjestysluku on 39448, koska näiden päivämäärien välisenä aikana on kulunut 39 447 päivää.

• Tilityspäivämäärä on päivä, jolloin ostaja hankkii arvopaperin, kuten joukkovelkakirjan. Erääntymispäivämäärä on päivä, jolloin arvopaperi vanhentuu. Oletetaan, että 30 vuoden joukkovelkakirja lasketaan liikkeelle 1.1.2008 ja ostetaan puoli vuotta myöhemmin. Liikkeellelaskemispäivämäärä olisi 1.1.2008, tilityspäivämäärä 1.7.2008 ja erääntymispäivämäärä 1.1.2038, joka on 30 vuotta liikkeellelaskemispäivämäärän 1.1.2008 jälkeen.

• Tilityspvm, erääntymispvm, korkojakso ja peruste katkaistaan kokonaisluvuiksi.

• Jos tilityspvm, erääntymispvm, asettamispvm tai ens_korko ei ole kelvollinen päivämäärä, PARITON.ENS.NIMELLISARVO palauttaa #ARVO! ‑virhearvon.

• Jos korko < 0 tai tulos < 0, PARITON.ENS.NIMELLISARVO palauttaa #LUKU! ‑virhearvon.

• Jos peruste < 0 tai peruste > 4, PARITON.ENS.NIMELLISARVO palauttaa #LUKU! ‑virhearvon.

• Jos seuraava päivämääriä koskeva ehto ei toteudu, PARITON.ENS.NIMELLISARVO palauttaa #LUKU! ‑virhearvon.

  erääntymispvm > ens_korko > tilityspvm > liikkeellelaskupvm

• PARITON.ENS.NIMELLISARVO lasketaan seuraavasti:

  Jos ensimmäinen kausi on lyhyt:

  

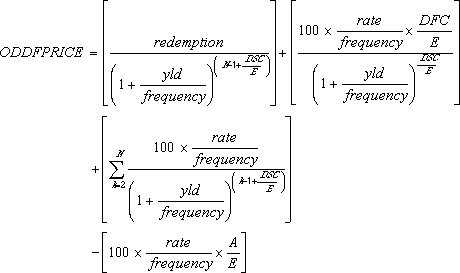
  jossa

  • A = päivien määrä korkojakson alusta tilityspäivään (kertyneiden päivien lukumäärä).

  • DSC = tilityspäivän ja seuraavan koronmaksupäivän välisen ajanjakson päivien määrä.

  • DFC = normaalista poikkeavan ensimmäisen korkokauden alun ja ensimmäisen koronmaksupäivän välisen ajanjakson päivien määrä.

  • E = korkojakson päivien määrä.

  • N = maksettavien korkosuoritusten määrä tilitys- ja lunastuspäivämäärän välillä. (Luku korotetaan tarvittaessa kokonaisluvuksi.)

    Jos ensimmäinen kausi on pitkä:

    

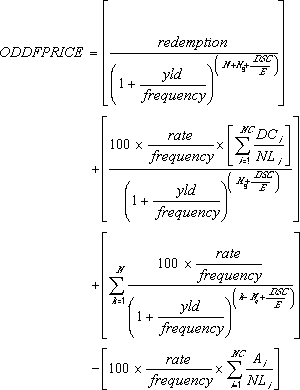
    jossa

  • Ai = päivien määrä laskettuna normaalista poikkeavan korkokauden i:nnen eli viimeisen näennäiskorkokauden alusta.

  • DCi = päivien määrä laskettuna nimetystä päivästä (tai liikkeellelaskupäivästä) ensimmäiseen näennäiseen koronmaksupäivään saakka (i = 1) tai näennäiskorkokauden päivien määrä (i = 2, ..., i = NC).

  • DSC = päivien määrä tilityspäivästä seuraavaan koronmaksupäivään.

  • E = koronmaksukauden päivien määrä.

  • N = maksettavien korkosuoritusten määrä ensimmäisen todellisen koronmaksupäivän ja lunastuspäivän välillä. (Luku korotetaan tarvittaessa kokonaisluvuksi.)

  • NC = normaalista poikkeavan korkokauden näennäiskorkokausien määrä. (Luku korotetaan tarvittaessa kokonaisluvuksi.)

  • NLi = normaali päivien määrä normaalista poikkeavan korkokauden kokonaisella i:nnellä eli viimeisellä näennäiskorkokaudella.

  • Nq = Kokonaisten näennäiskorkokausien määrä tilityspäivämäärän ja ensimmäisen koronmaksupäivän välillä.

Esimerkki

Kopioi esimerkkitiedot seuraavaan taulukkoon ja lisää se uuden Excel‑laskentataulukon soluun A1. Kaavat näyttävät tuloksia, kun valitset ne, painat F2-näppäintä ja sitten Enter-näppäintä. Voit säätää sarakkeiden leveyttä, että näet kaikki tiedot.