Solveri kasutamine kapitali eelarvestamiseks

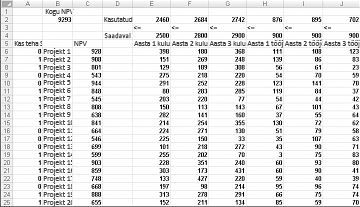
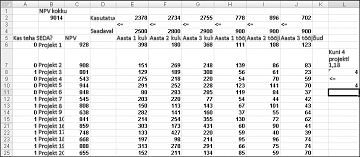
Enamik korporatsioone soovib teostada projekte, mis panustavad suurimasse nüüdisväärtusse (NPV), kasutades piiratud ressursse (tavaliselt kapitali ja tööjõudu). Oletame, et tarkvaraarendusettevõte püüab kindlaks teha, milliseid 20 tarkvaraprojekti ta peaks tegema. NPV (miljonites dollarites) on panustatud nii iga projekti kui ka kapitali (miljonites dollarites) ja programmeerimisvahendite arv, mida on vaja iga järgmise kolme aasta jooksul, on esitatud töölehel Põhimudel faili Capbudget.xlsx, mis on näidatud järgmisel lehel joonisel 30–1. Näiteks project 2 annab 908 miljonit dollarit. See nõuab 1. aastal 151 miljonit dollarit, 269 miljonit dollarit 2. aastal ja 248 miljonit dollarit 3. aastal. Projektis 2 nõutakse 1. aastal 139 programmeerijat, 2. aastal 86 programmeerijat ja 3. aastal 83 programmeerijat. Lahtrites E4:G4 kuvatakse igal kolmel aastal saadaolev kapital (miljonites dollarites) ja lahtrid H4:J4 näitavad, kui palju programmeerijaid on saadaval. Näiteks on 1. aastal saadaval kuni 2,5 miljardit dollarit kapitali ja 900 programmeerijat.

Äriühing peab otsustama, kas ta peaks teostama iga projekti. Oletame, et me ei saa teha murdosa tarkvaraprojektist; Kui eraldame näiteks 0,5 vajalikest ressurssidest, oleks meil mittetöötav programm, mis tooks meile 0 $tulu!

Modelleerimissituatsioonides, kus te kas midagi teete või ei tee, on kasutada kahendmuutvaid lahtreid. Kahendmuutev lahter võrdub alati 0 või 1. Kui projektile vastava kahendmuutmislahtri väärtus on 1, teeme projekti. Kui projektile vastava kahendmuutmislahtri väärtus on 0, ei tee me projekti. Solveri saate häälestada kasutama kahendmuutvate lahtrite vahemikku, lisades piirangu – valige muutuvad lahtrid, mida soovite kasutada, ja seejärel valige dialoogiboksi Piirangu lisamine loendist Bin.

Sellel taustal oleme valmis tarkvaraprojekti valiku probleemi lahendama. Nagu Solveri mudeli puhul, saamegi alustada sihtlahtri, muutuvate lahtrite ja piirangute tuvastamisega.

• Sihtlahter. Maksimeerime valitud projektide loodud NPV-d.

• Lahtrite muutmine. Otsime iga projekti jaoks 0 või 1 kahendlahtrit. Asusin need lahtrid vahemikus A6:A25 (ja nimetasin vahemiku nimeks doit). Näiteks lahtris A6 olev 1 osutab, et me võtame projekti 1; lahtris C6 olev 0 näitab, et me ei võta projekti Project 1 endale.

• Piirangud. Peame tagama, et iga aasta t (t=1, 2, 3) puhul on kasutatud aasta t kapital väiksem või võrdne aasta t kapitali kättesaadavusega ja aasta t kasutamine on väiksem või võrdne aasta t tööjõuga.

Nagu näete, peab meie tööleht arvutama projektivalikute kohta NPV, kasutatud kapitali aastas ja programmeerijad igal aastal. Lahtris B2 kasutan valitud projektide genereeritud NPV koguarvu arvutamiseks valemit SUMPRODUCT(doit,NPV ). (Vahemiku nimi NPV viitab vahemikule C6:C25.) Iga projekti puhul, mille veerus A on 1 arv 1, korjab see valem ära projekti NPV ja iga projekti puhul, mille veerus A on 0 0, ei võta see valem projekti NPV-d. Seetõttu saame arvutada kõigi projektide NPV-d ja meie sihtlahter on lineaarne, kuna see arvutatakse vormile järgnevate terminite summeerimise teel*(konstant). Samamoodi arvutan igal aastal kasutatud kapitali ja igal aastal kasutatud tööjõu, kopeerides lahtritest E2 lahtrisse F2:J2 valemi SUMPRODUCT(doit,E6:E25).

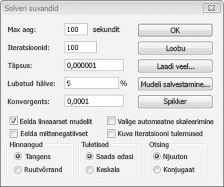
Nüüd täidan dialoogiboksi Solveri parameetrid, nagu on näidatud joonisel 30–2.

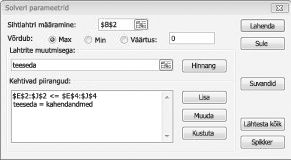
Meie eesmärk on maksimeerida valitud projektide NPV-d (lahter B2). Meie muutuvad lahtrid (vahemik nimega doit) on iga projekti kahendlahtrid. Piirang E2:J2<=E4:J4 tagab, et igal aastal on kasutatud kapital ja tööjõud väiksemad või võrdsed saadaoleva kapitali ja tööjõuga. Muutuvate lahtrite kahendarvuks muutva piirangu lisamiseks klõpsake dialoogiboksis Solveri parameetrid nuppu Lisa ja seejärel valige dialoogiboksi keskel olevast loendist Suvand Bin. Dialoogiboks Piirangu lisamine peaks olema kuvatud joonisel 30–3 kujutatud viisil.

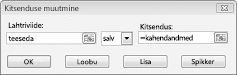
Meie mudel on lineaarne, kuna sihtlahter arvutatakse vormiga terminite summana *(konstant) ja kuna ressursikasutuse piirangud arvutatakse, võrreldes (muutuvate lahtrite) summat*(konstante) konstandiga.

Kui dialoogiboks Solveri parameetrid on täidetud, klõpsake nuppu Lahenda ja tulemused on kuvatud joonisel 30–1 eespool. Ettevõte võib saada maksimaalselt 9,293 miljonit dollarit (9,293 miljardit dollarit), valides projektid 2, 3, 6–10, 14–16, 19 ja 20.

Mõnikord on projektivaliku mudelitel muid piiranguid. Oletagem näiteks, et kui valime project 3, peame valima ka project 4. Kuna meie praegune optimaalne lahendus valib Project 3, kuid mitte Project 4, teame, et meie praegune lahendus ei saa jääda optimaalseks. Selle probleemi lahendamiseks lisage lihtsalt piirang, et Project 3 binaarmuutmislahter on väiksem või võrdne Project 4 kahendmuutva lahtriga.

Selle näite leiate faili Capbudget.xlsx töölehelt If 3 siis 4 , mis on kujutatud joonisel 30–4. Lahter L9 viitab Project 3-ga seotud kahendväärtusele ja lahtrile L12 Project 4 seotud kahendväärtusele. Kui lisame piirangu L9<=L12, siis kui valime Project 3, siis L9 võrdub 1 ja meie kitsendus sunnib L12 (Project 4 binaarfaili) 1-ga võrdseks. Kui me project 3 ei vali, peab meie piirang project 4 muutuvasse lahtrisse jätma kahendväärtuse. Kui me ei vali rakendust Project 3, võrdub L9 väärtusega 0 ja meie kitsendus võimaldab Project 4 binaarfailil võrdub 0 või 1, mis on see, mida me tahame. Uus optimaalne lahendus on näidatud joonisel 30–4.

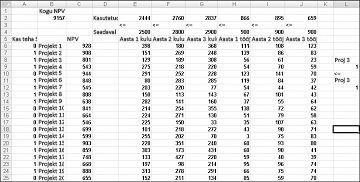
Uus optimaalne lahendus arvutatakse siis, kui valite Project 3, tähendab, et peame valima ka Project 4. Oletagem nüüd, et saame teha ainult nelja projekti projektide 1–10 hulgast. (Vt töölehte Kõige rohkem 4 P1–P10 , näidatud joonisel 30–5.) Lahtris L8 arvutame projektidega 1 kuni 10 seotud kahendväärtuste summa valemiga SUM(A6:A15). Seejärel lisame piirangu L8<=L10, mis tagab, et valitud on kuni 4 esimest 10 projekti. Uus optimaalne lahendus on näidatud joonisel 30–5. NPV on langenud 9,014 miljardi dollarini.

Lineaarseid Solveri mudeleid, kus osa või kõik muutuvad lahtrid peavad olema kahend- või täisarvud, on tavaliselt keerulisem lahendada kui lineaarseid mudeleid, kus kõik muutuvad lahtrid võivad olla murrud. Seetõttu oleme sageli rahul kahend- või täisarvulise programmeerimisprobleemi peaaegu optimaalse lahendusega. Kui teie Solveri mudel töötab pikka aega, võiksite kaaluda dialoogiboksi Solveri suvandid sätte Kõikumine reguleerimist. (Vt joonis 30–6).) Näiteks 0,5% säte Kõikumine tähendab, et Solver lõpetab esimese korra, kui leiab sobiva lahenduse, mis jääb 0,5 protsendi piiresse teoreetilise optimaalse sihtlahtri väärtusest (teoreetiline optimaalne sihtlahtriväärtus on optimaalne sihtväärtus, mis leitakse siis, kui kahend- ja täisarvulised piirangud on ära jäetud). Sageli seisame silmitsi valikuga, kas leida vastus 10 minuti jooksul 10 protsendi jooksul optimaalsest või leida optimaalne lahendus arvutiaja kahe nädala jooksul! Vaikehälbe väärtus on 0,05%, mis tähendab, et Solver peatub, kui leiab sihtlahtri väärtuse 0,05% piires teoreetiliselt optimaalsest sihtlahtriväärtusest.

1. Ettevõttel on kaalumisel üheksa projekti. Järgmises tabelis on esitatud iga projekti lisatav NPV ja iga projekti jaoks järgmise kahe aasta jooksul nõutav kapital. (Kõik arvud on miljonites.) Näiteks lisab Projekt 1 NPV-sse 14 miljonit dollarit ja nõuab 1. aasta jooksul 12 miljonit dollarit ja 2. aasta jooksul 3 miljonit dollarit. 1. aastal on projektide jaoks saadaval 50 miljonit dollarit kapitali ja 2. aasta jooksul on see saadaval 20 miljonit dollarit.

	NPV	1. aasta kulud	2. aasta kulud
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Kui me ei saa teha murdosa projektist, kuid peame teostama kas kogu projekti või mitte ühtegi projekti, siis kuidas me saame NPV-d maksimeerida?

• Oletagem, et project 4 käivitamisel tuleb kasutada projekti 5. Kuidas saame NPV-d maksimeerida?

• Kirjastus püüab kindlaks teha, millisest 36-st raamatust peaks ta sel aastal välja andma. Faili Pressdata.xlsx annab iga raamatu kohta järgmist teavet.

  • Prognoositud tulud ja arenduskulud (tuhandetes dollarites)

  • Iga raamatu lehed

  • Kas raamat on suunatud tarkvaraarendajate sihtrühmale (tähistatud veerus E oleva 1-ga)

    Kirjastus saab sel aastal avaldada kuni 8500 lehekülge sisaldavaid raamatuid ja peab avaldama tarkvaraarendajatele suunatud vähemalt neli raamatut. Kuidas saab ettevõte oma kasumit maksimeerida?

Seda artiklit on kohandanud Microsoft Office Excel 2007 andmeanalüüs ja äri modelleerimine Wayne L. Winston poolt.

See klassiruumi stiilis raamat on välja töötatud selliste esitluste sarjast, mille on koostanud tuntud statistikust ja äriprofessorist Wayne Winston, kes on spetsialiseerunud Exceli loomingulistele ja praktilisttele rakendustele.