Märkus.: Soovime pakkuda teie keeles kõige ajakohasemat spikrisisu niipea kui võimalik. See leht on tõlgitud automaatselt ja sellel võib leiduda grammatikavigu või ebatäpsusi. Tahame, et sellest sisust oleks teile abi. Palun märkige selle lehe allservas, kas sellest teabest oli teile kasu või mitte. Soovi korral saab ingliskeelset artiklit lugeda siit.
Selles artiklis käsitletakse Solveri abil, Microsoft Exceli lisandmooduli programmi saate mõjuanalüüsi, on optimaalse toote mix määratlemiseks.
Kuidas kindlaks teha kuu toote mix, mis maksimeerib tasuvust?
Ettevõtetes sageli vaja kindlaks teha, andes igakuiselt iga toote kogus. Lihtsaim kujul toote segada probleem hõlmab kindlaks määrata iga toote, mis tuleb koostada kuul, kasumi maksimeerimiseks tehke järgmist. Toodete tavaliselt peab kinni järgmistest:
-
Toodete ei saa kasutada rohkem ressursse on saadaval.
-
Seal on iga toote jaoks piiratud nõudmine. Me ei saa aedvili mitu toodet kuul, kui nõudmisel dikteerib, kuna liigne on raisatud (nt rikneva uimastitega).
Vaatame nüüd lahendada mix näidistulemid järgmises näites. Selle probleemi lahendamiseks leiate faili Prodmix.xlsx, mis on näidatud joonisel 27-1.
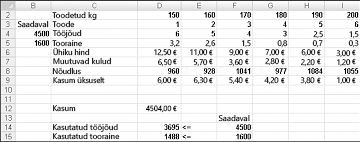
Oletame, et töötame uimastitega andev kuus eri toodete lubamist oma ettevõtte jaoks. Iga toote jaoks on vaja töö ja materjali. Rea 4 joonis 27-1 näitab töö vajaminev trellid iga toote tundi ja rida 5 naela vajaminev trellid iga toote materjali. Näiteks toodavad trellid toote 1 nõuab kuus tundi tööd ja 3,2 naela materjali. Iga uimastitega trellid hind on esitatud rida 6, trellid ühiku maksumus on antud Real 7 ja kasum toetus trellid kohta on esitatud reas 9. Näiteks toode 2 müüs $11.00 kohta trellid eest, andmesidekasutusele $5,70 kohta trellid ühikuhind ja aitab $5,30 kasum trellid kohta. Selle kuu järele vahel on esitatud rida 8. Näiteks nõudmisel toode 3 on 1041 £. See kuu, 4500 tundi tööd ja 1 600 naela materjali on saadaval. Kuidas saab selle ettevõtte selle kuu kasumi maksimeerimiseks?
Kui soovime teadis midagi Exceli lisandmoodul Solver, me ehitada töölehe jälgida kasumi- ja ressursihalduse kasutamine seotud toote mix ründavad probleemi. Seejärel me kasutaks katse ja vea toote mix optimeerida kasum ilma rohkem töö või kui see on saadaval materjali abil ja vajadusel üle mõne ravimi toodavad muuta. Kasutame Solveri selle protsessi üksnes etapis prooviversiooni tõrge. Sisuliselt on Solveri optimeerimine otsimootori, mis sooritavad tõrgeteta prooviversiooni-vea otsing.
Toote mix probleemi lahendamiseks klahvi on tõhus arvutada ressursikasutus ja seostatud iga toote segada kasum. Tööriist, mille soovime abil muuta selle arvutuse on funktsiooni SUMPRODUCT. Funktsioon SUMPRODUCT korrutab lahtrivahemike vastavate väärtuste ja tagastab nende väärtuste summa. Iga lahtrivahemik, mida kasutatakse SUMPRODUCT hindamise peab olema sama mõõtmed, mis tähendab, et saate SUMPRODUCT kaks rida või kaks veergu, kuid mitte ühte veergu ja ühte rida.
Näide sellest, kuidas kasutame funktsiooni SUMPRODUCT meie toode mix näide, proovime nüüd meie ressursikasutus arvutada. Meie töö kasutamine arvutamisel
(Töö kohta trellid uimastitega 1) + *(Drug 1 pounds produced) (töö kohta trellid uimastitega 2) * (ravimi toodeti 2 naela) +... (Töö kohta trellid uimastitega 6) * (ravimi 6 naela toodeti)
Me võib arvutada töö kasutus töömahukam viisil kui D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4. Samuti võib materjali kasutus arvutatakse järgmiselt D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + I2 * I5. Need valemid sisestamine töölehel kuus toodete on aeganõudev. Kujutage ette, kui kaua võtab kui töötasite ettevõte, mis toodab, näiteks 50 toodete nende taimest. Kopeerida D14 D15 SUMPRODUCT($D$2:$I$2,D4:I4)valem on palju lihtsama arvutada töö ja materjali kasutamist. See valem arvutab D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * I4 (mis on meie töö kasutamine), kuid märksa lihtsam sisestage! Pange tähele, et kasutada märk $ vahemiku D2:I2 nii, et valemi kopeerimisel ma ikka jäädvustada toote mix rea 2. D15 lahtri valem arvutab materjali kasutus.
Sarnasel viisil meie kasum määratud
(Ravimi 1 kasum trellid kohta) * (toodetud naela uimastitega 1) + (uimastitega 2 kasum kohta trellid) * (ravimi toodeti 2 naela) +... (Uimastitega 6 kasum kohta trellid) * (ravimi 6 naela toodeti)
Kasumi hõlpsalt arvutatakse valemiga SUMPRODUCT(D9:I9,$D$2:$I$2)lahtris D12.
Nüüd saate tuvastada meie toote mix Solveri mudeli kolm osa.
-
Sihtlahter.Meie eesmärk on (arvutatud lahtris D12) kasumi maksimeerimiseks.
-
Muutuvad lahtrid.Arvu naela toodeti iga toote (loetletud lahtrivahemik D2:I2)
-
Piiranguid. Meil on järgmised piirangud:
-
Ärge kasutage rohkem töö või materjali kui on saadaval. Väärtused lahtrite D14:D15 (kasutatavate ressursside) peab olema väiksem kui või võrdne väärtused lahtrite F14:F15 (ressursid).
-
Ei tooda rohkem kui on vajadusel ravimi. St väärtused lahtrite D2:I2 (naela toodeti iga uimastitega) peab olema väiksem kui või võrdne järele (loetletud lahtrite D8:I8) vahel.
-
Meil miinusmärgiga mõne ravimi ei teki.
-
Ma näitan saate sisestada Sihtlahter, kuidas muuta lahtrite ja piiranguid Solver. Seejärel tegemiseks on vaja kasumi maksimeerimine toote mix otsimiseks nuppu Lahenda!
Alustamiseks klõpsake vahekaarti andmed ja analüüs nuppu Solver.
Märkus.: Nagu peatükk 26 "An Sissejuhatus abil optimeerimine koos Exceli lisandmoodul Solver," Solveri on installitud, klõpsake Microsoft Office'i nuppu, seejärel Exceli suvandid, millele järgneb lisandmoodulid. Klõpsake loendi Halda väärtust Exceli lisandmoodulid, märkige ruut lisandmoodul Solver ja seejärel klõpsake nuppu OK.
Kuvatakse dialoogiboks Solveri parameetrid, nagu on näidatud joonisel 27 – 2.
Klõpsake välja seadmine Sihtlahter ja seejärel valige meie kasum lahtrit (lahtrit D12). Klõpsake välja lahtrite muutmise teel ja siis osutage valikule vahemiku D2:I2, mis sisaldab iga uimastitega toodeti naela. Dialoogiboks peaks välja nägema nüüd joonis 27-3.
Nüüd olete valmis lisada piiranguid mudel. Klõpsake nuppu Lisa. Kuvatakse dialoogiboksi lisamine piirang, näidatud joonisel 27-4.
Kasutus ressursipiirangute lisamiseks käsku Lahtrilink lahtriviide väljale ja seejärel valige andmevahemik D14:D15. Valige < = keskmisel loendist. Klõpsake väljal piirang ja seejärel valige lahtrivahemik, F14:F15. Piirangu lisamiseks dialoogiboksi nüüd peaks välja nägema umbes joonis 27-5.
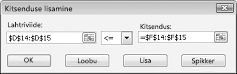
Meil on nüüd tagada, et kui Solveri üritab erinevate väärtuste muutmise lahtrid, ainult kombinatsioonid, mis vastavad nii D14< = F14 (töö kasutatud on väiksem või võrdne töömahukust, mis on saadaval) ja D15< = F15 (kasutatud on väiksem või võrdne käsitletakse materjali saadaval). Klõpsake nuppu Lisa ja sisestage vajadusel piiranguid. Täitke dialoogiboksi lisamine piirang nagu on näidatud joonisel 27 – 6.
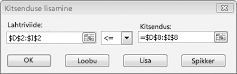
Need piirangud lisamine tagab, et kui Solveri püüab erinevate kombinatsioonide muutmisega lahtriväärtused, ainult kombinatsioonid, mis vastavad järgmiste parameetrite käsitletakse:
-
D2< = D8 (tulemuseks uimastitega 1 summa on väiksem kui või võrdne järele uimastitega 1)
-
E2< = E8 (toodeti uimastitega 2 on väiksem kui või võrdne nõudmisel uimastitega 2)
-
F2< = F8 (tulemuseks uimastitega 3 tehtud summa on väiksem kui või võrdne järele uimastitega 3)
-
G2< = G8 (tulemuseks tehtud uimastitega 4 summa on väiksem kui või võrdne järele uimastitega 4)
-
H2< = H8 (tulemuseks uimastitega 5 tehtud summa on väiksem kui või võrdne järele uimastitega 5)
-
I2< = I8 (tulemuseks uimastitega 6 tehtud summa on väiksem kui või võrdne järele uimastitega 6)
Dialoogiboksi piirangu lisamiseks klõpsake nuppu OK. Solveri akna peaks välja nägema umbes joonis 27-7.
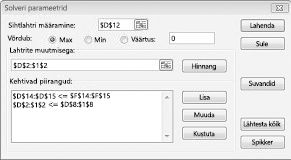
Sisestage piirang, mis muutuvad lahtrid peab olema negatiivne dialoogiboksi Solveri suvandid. Klõpsake dialoogiboksi Solveri parameetrid nuppu Suvandid. Kontrollige väljal endale lineaarse mudeli ja endale, mitte-negatiivne välja nagu on näidatud järgmisel lehel joonis 27-8. Klõpsake nuppu OK.
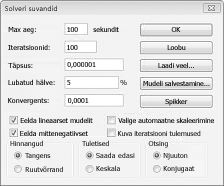
Oletame, mitte-negatiivne ruudu tagab Solveri leiab ainult kombinatsioonid muutuvad lahtrid, kus iga muutmisega lahtri eeldab negatiivne väärtus. Me märgitud välja endale lineaarse mudeli, kuna toote segada probleem on Solveri probleemi nimetatakse lineaarse mudelieri tüüpi. Solveri mudeli on sisuliselt lineaarse järgmistes olukordades:
-
Lisades vormi tingimused on arvutatud Sihtlahter (muutmise cell)*(constant).
-
Iga piirang vastab "lineaarse mudeli nõue." See tähendab, et hinnatakse iga piirang lisades vormi tingimused (muutmise cell)*(constant) ja võrdlemine konstandi summad.
Miks on see probleem Solveri lineaarse? Meie Sihtlahter (kasum) arvutatakse järgmiselt
(Ravimi 1 kasum trellid kohta) * (toodetud naela uimastitega 1) + (uimastitega 2 kasum kohta trellid) * (ravimi toodeti 2 naela) +... (Uimastitega 6 kasum kohta trellid) * (ravimi 6 naela toodeti)
Selle arvutuse järgib, kus on tuletatud target lahtri väärtuse, lisades vormi mustri (muutmise cell)*(constant).
Meie töö piirang hinnatakse saadud (töö kohta trellid uimastitega 1) väärtust * (toodetud naela uimastitega 1) + (töö kohta trellid uimastitega 2) *(Drug 2 pounds produced) +... (Töö meilede kohta trellid uimastitega 6) * (ravimi 6 naela toodeti) töö, mis on saadaval.
Seetõttu, lisades vormi tingimused hinnatakse töö piirang (muutmise cell)*(constant) ja võrdlemine konstandi summad. Töö piirang nii materjali piirang vastama lineaarse mudeli nõue.
Meie nõudmisel piiranguid vormis
(Uimastitega 1 toodeti) < = (uimastitega 1 nõudmisel) (toodeti uimastitega 2) < (vajadusel uimastitega 2) = § (uimastitega 6 toodeti) < = (uimastitega 6 nõudmisel)
Iga nõudmisel piirang vastab lineaarse mudeli nõue, kuna iga hinnatakse, lisades vormi tingimused (muutmise cell)*(constant) ja võrdlemine konstandi summad.
On näidatud, et meie toote mix mudel on lineaarne mudel, miks peaks me sellest?
-
Solveri mudeli on lineaarne ja endale lineaarse mudeli valimiseks Solveri on tagatud Solveri mudeli optimaalse lahenduse leidmiseks. Kui mudeli Solver pole lineaarne, Solveri võib või võib leida optimaalne lahendus.
-
Kui mudeli Solveri on lineaarne ja valige endale lineaarse mudeli, kasutab Solveri mudeli optimaalsete lahenduste leidmiseks väga tõhusa algoritmi (simplex meetod). Kui mudeli Solveri on lineaarne ja me ei Vali endale lineaarse mudeli, Solver kasutab väga ebaefektiivne algoritmi (GRG2 meetod) ja võib-olla raske leida mudeli optimaalne lahendus.
Pärast nupu OK klõpsamist klõpsake dialoogiboksi Solveri suvandid, me naasta peamised Solveri kuvatud dialoogiboksi, varem sisse joonis 27-7. Kui me nuppu Lahenda, Solveri arvutab optimaalne lahendus (kui see on olemas) meie toote mix mudel. Nagu märgitud Peatükk 26, oleks optimaalse lahenduse toote mix mudeli muutmise Lahtriväärtuste (naela toodeti iga uimastitega) komplekt, mis maksimeerib kasumi kogumi kõik teostatav lahendused. Uuesti, on võimalik lahendus kogumi vasta kõik piiranguid lahtriväärtuste muutmine. Joonis 27-9 muutmisega lahtri väärtused on võimalik lahendus, sest on kõik negatiivne, ei ületa tootmistaseme nõudmisel ja ressursikasutus ei ületa saadaval ressursid.
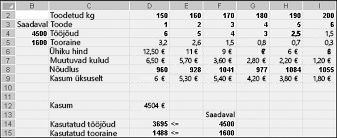
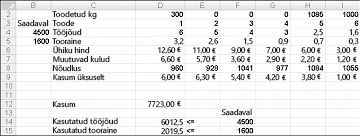
Näidatud joonisel 27-10 järgmisel lehel muutmisega lahtriväärtuste tähistada järgmistel põhjustel võimatu lahendus on:
-
Me tootma rohkem kui nõudmisel seda uimastitega 5.
-
Kasutame veel töömahukust, mis on saadaval.
-
Kasutame materjali rohkem kui on olemas.
Pärast nupu lahenda, Solveri kiiresti optimaalse lahenduse, mis on näidatud joonisel 27-11. Peate valima Säilita Solveri lahend säilitada optimaalse väärtuste töölehel.
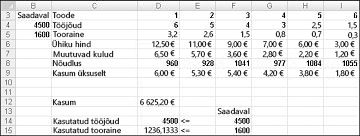
Meie uimastitega ettevõtte saate selle kuu kasum $6,625.20 tasemel maksimeerimine esitamisega 596.67 naela uimastitega 4, 5 uimastitega 1084 naela ja ükski muu narkootikume! Me ei saa määrata, kui me saavutada maksimaalne kasum $6,625.20 muul viisil. Kõik me võib olla kindel, et on meie piiratud ressursid ja vajadusel, on kuidagi sel kuul rohkem kui 6,627.20 teha.
Oletame, et järele iga toote peab olema täidetud. (Vt Pole võimalik lahendus töölehe failis Prodmix.xlsx). Oleme siis meie nõudmisel piiranguid kaudu muuta D2:I2< = D8:I8 et D2:I2> = D8:I8. Selleks, avage Solveri, valige soovitud D2:I2< = D8:I8 piirang, ja seejärel klõpsake käsku Muuda. Kuvatakse dialoogiboks Muuda piirang, näidatud joonisel 27-12.
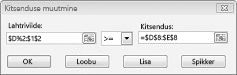
Valige > = ja seejärel klõpsake nuppu OK. Me olete nüüd tagada Solveri arvestab muuta ainult lahtri väärtuste, kõik nõudmistele vastavad. Kui klõpsate nuppu Lahenda, kuvatakse teade "Solver ei leidnud võimalik lahendus." See teade ei tähenda, mida me tehtud vea meie mudelit, kuid pigem mis meie piiratud ressursside, me ei saa rahuldamiseks kõigist toodetest. Solveri on lihtsalt meile, et kui soovime iga toote rahuldamiseks, läheb vaja lisada veel töömahukust, rohkem tooraine või nii mitu.
Vaatame, mis juhtub, kui me lubada piiramatu nõudmisel iga toote ja me lubada negatiivne koguseid tuleb luua iga uimastitega. (Näete Solveri probleemi failis Prodmix.xlsx töölehel Määrata väärtused on koondu .) Optimaalse lahenduse leidmiseks olukord Solveri avada, klõpsake nuppu Suvandid ja tühjendage ruut endale mitte-negatiivsed. Valige dialoogiboksi Solveri parameetrid piirangut nõudmisel D2:I2< = D8:I8 ja klõpsake nuppu Kustuta piirangut eemaldada. Kui klõpsate nuppu Lahenda, Solveri tagastab sõnum "Lahtri väärtused koondu." See teade tähendab, et kui Sihtlahter (nagu siinses näites) suurendada, on meelevaldselt suurte target lahtriväärtuste teostatav lahendusi. (Kui Sihtlahter minimeerida, sõnum "Määrata lahtri väärtused on koondu" tähendab, on võimalik lahendusi meelevaldselt väikese eesmärgi lahtri väärtusega.) Meie olukorda, negatiivne koostamine ravimi, võimaldades tegelikult "loome" ressursid, millest saab kasutada andes meelevaldselt suure hulga ravimitega. Antud meie piiramatu nõudmisel, see võimaldab meil teha piiramatu kasum. Tegelikku olukorda, ei saa teha raha lõpmatu summa. Lühidalt, kui näete "Seadmine väärtused on koondu", mudelisse on viga.
-
Oletame, et ettevõte uimastitega saate osta kuni 500 tundi $ 1 tund enamat praeguse tööjõukulude tööd. Kuidas me kasumi maksimeerimiseks?
-
Kiip tootmismeeskondadel taimest, neli tehnikud (A, B, C ja D) esitavad kolme products (tooted 1, 2 ja 3). See kuu, chip tootja saate müüa 80 ühikut toote 1, 50 toode 2, ja kõige 50 toode 3. Tehnik A saate teha ainult toodete 1 – 3. Tehnik B saate teha ainult toodete 1 ja 2. Tehnik C saate teha ainult toode 3. Tehnik D saab teha ainult toode 2. Iga üksuse toodetud, toodete aitavad järgmised kasum: toote 1, $6; Toode 2, $7; ja toode 3, $10. Aeg (tundides) iga tehnik peab toote valmistamine on järgmine:
Toode
Tehnik A
Tehnik B
Tehnik C
Tehnik D
1
2
2,5
Ei saa teha
Ei saa teha
2
Ei saa teha
3
Ei saa teha
3,5
3
3
Ei saa teha
4
Ei saa teha
-
Iga tehnik saate töötada kuni 120 tundi kuus. Kuidas saab kiibi tootja selle kuu kasumi maksimeerimiseks? Oletame, et andmepunktide üksuste saate esitada.
-
Arvuti tootmismeeskondadel taimest toodab hiir, klaviatuur ja video mängu juhtkangi on siiani. Järgmises tabelis on esitatud ühiku kasum, ühiku töö kasutus, kuu nõudmisel ja ühiku arvuti kellaaja kasutus:
Hiir
Klaviatuur
Juhtkangi on siiani
Kasumi ühiku
$8
$11
$9
Labor kasutus ühiku
.2 tund
.3 tund
.24 tunni
Seadme ajaühiku
.04 tund
.055 tund
.04 tund
Igakuine nõudmisel
15 000
27000
11 000
-
Iga kuu kokku 13 000 töö tundi ja 3000 tundi seadme aega on saadaval. Kuidas tootja maksimeerimine selle kuu kasum osakaal ettevõttest?
-
Lahendada meie uimastitega näide eeldades minimaalne nõudmisel 200 tk iga ravimi peavad olema täidetud.
-
Jason teeb rombi käevõrud, kaelakeed ja kõrvarõngad. Ta soovib 160 tundi kuus. Ta on 800 untsi ruutu. Kasumi, töö aeg ja esitama iga toote ruutu untsi on esitatud allpool. Kui nõudmisel iga toote jaoks on piiramatult, kuidas saate Jason oma kasumi maksimeerimiseks?
Toode
Üksuse kasum
Labor tundi ühiku kohta
Untsi ruutu ühiku kohta
Käevõru
300 €
.35
1,2
Kaelakee
200 €
.15
.75
Kõrvarõngad
100 €
0,05
.5










