ODDFPRICE

Kirjeldus

Tagastab hinna väärtpaberi 100-eurose nominaalväärtuse kohta ebastandardse (pika või lühikese) esimese perioodi korral.

Süntaks

ODDFPRICE(tehing, tähtaeg, väljastus, esimene_kupong, määr, tootlus, tagastusväärtus, sagedus, [alus])

Funktsiooni ODDFPRICE süntaks sisaldab järgmisi argumente.

• Tehing    – nõutav. Väärtpaberitehingu kuupäev. Väärtpaberitehingu kuupäev on emissioonijärgne kuupäev, mil väärtpaber müüakse ostjale.

• Tähtaeg    – nõutav. Väärtpaberi tagasimaksetähtaeg. Tagasimaksetähtaeg on kuupäev, mil väärtpaber saab maksekohustuse.

• Emissioon    – nõutav. Väärtpaberi emissiooni kuupäev.

• Esimene_kupong    – nõutav. Väärtpaberi esimene intressiarvutuspäev.

• Määr – nõutav. Väärtpaberi intressimäär.

• Tootlus    – nõutav. Väärtpaberi aastane tootlus.

• Tagastushind    – nõutav. Väärtpaberi tagastusväärtus 100-kroonise nominaalväärtuse kohta.

• Sagedus    – nõutav. Kupongimaksete arv aastas. Aastaste maksete korral on sagedus 1; poolaastaste korral 2; kvartalimaksete korral 4.

• Alus    – valikuline. Kasutatav päevaarvestusaluse tüüp.

Kommentaarid

• Microsoft Excel salvestab kuupäevi järjestikuste järjenumbritena, nii saab neid kasutada arvutustes. Vaikimisi on 1. jaanuari 1900 järjenumbriks 1 ning 1. jaanuari 2008 järjenumbriks 39448, kuna see on 39448 päeva pärast 1. jaanuarit 1900.

• Tasakaalutuse kuupäev on kuupäev, mil ostja omandab mõne kupongi (nt võlakirja). Tähtaja kuupäev on kuupäev, mil kupong saab aegub. Oletame näiteks, et 30-aastane võlakiri väljastatakse 1. jaanuaril 2008 ning see ostetakse kuus kuud hiljem. Väljastamise kuupäevaks on 1. jaanuar 2008, tasakaalustuse kuupäevaks on 1. juuli 2008 ning tähtaja kuupäevaks on 1. jaanuar 2038, mis on 30 aastat pärast väljastamise kuupäeva (1. jaanuar 2008).

• Tehingu, tähtaja, emissiooni, esimese_kupongi ja aluse murdosa kärbitakse.

• Kui tehing, tähtaeg, emissioon või first_coupon ei sobi kuupäevaks, tagastab funktsioon ODDFPRICE #VALUE! #NUM!.

• Kui määr < 0 või kui tootlus < 0, tagastab funktsioon ODDFPRICE #NUM! #NUM!.

• Kui alus < 0 või kui alus > 4, tagastab funktsioon ODDFPRICE #NUM! #NUM!.

• Järgmine kuupäevatingimus peab olema täidetud; vastasel juhul tagastab funktsioon ODDFPRICE #NUM! veaväärtus:

  tähtaeg > esimene_kupong > tehing > emissioon

• Funktsiooni ODDFPRICE arvutatakse järgmiselt:

  Ebastandardselt lühike esimene intressiperiood:

  

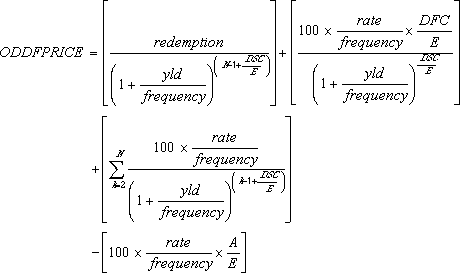
  kus

  • A = päevade arv intressiperioodi algusest tehingupäevani (viitepäevad).

  • DSC = päevade arv tehingupäevast järgmise intressiarvutuspäevani.

  • DFC = päevade arv ebastandardse pikkusega esimese intressiperioodi algusest esimese intressiarvutuspäevani.

  • E = päevade arv intressiperioodis.

  • N = maksmisele kuuluvate kupongide arv tehingupäeva ja tagasimaksetähtaja vahel. (Kui see arv sisaldab murdosa, ümardatakse see ülespoole järgmise täisarvuni.)

    Ebastandardselt pikk esimene intressiperiood:

    

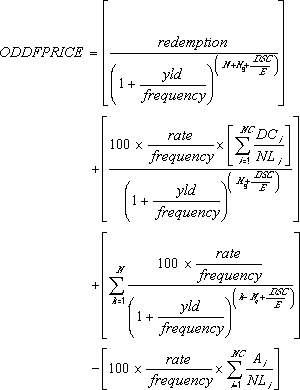
    kus

  • Ai = päevade arv ebastandardse pikkusega perioodi i-nda või viimase arvestusliku intressiperioodi algusest.

  • DCi = päevade arv kupongil olevast kuupäevast (või emissioonipäevast) esimese arvestusliku intressiarvutuspäevani (i = 1) või päevade arv arvestuslikus intressiperioodis (i = 2, ..., i = NC).

  • DSC = päevade arv tehingupäevast järgmise intressiarvutuspäevani.

  • E = päevade arv intressiperioodis.

  • N = maksmisele kuuluvate tegelike kupongide arv tehingupäeva ja tagasimaksetähtaja vahel. (Kui see arv sisaldab murdosa, ümardatakse see ülespoole järgmise täisarvuni.)

  • NC = ebastandardse pikkusega perioodi jäävate arvestuslike intressiperioodide arv. (Kui see arv sisaldab murdosa, ümardatakse see ülespoole järgmise täisarvuni.)

  • NLi = ebastandardse pikkusega perioodi sees olev terve i-nda või viimase arvestusliku intressiperioodi normaalne pikkus päevades.

  • Nq = täispikkusega arvestuslike intressiperioodide arv tehingupäeva ja esimese intressiarvutuspäeva vahel.

Näide.

Kopeerige järgmise tabeli näidisandmed ja kleepige need uue Exceli töölehe lahtrisse A1. Selleks et valemid näitaksid tulemeid, valige need, vajutage klahvi F2 ja seejärel vajutage sisestusklahvi (Enter). Vajaduse korral saate kogu teabe kuvamiseks veerulaiust muuta.