Uso de Solver para la presupuestación de capital

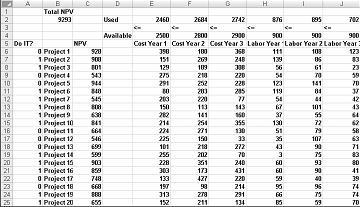
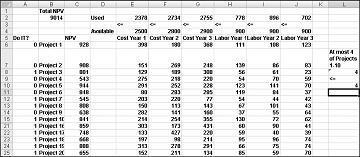
La mayoría de las empresas desean llevar a cabo proyectos que aporten el mayor valor neto actual (VNA), sujetos a recursos limitados (generalmente capital y mano de obra). Supongamos que una empresa de desarrollo de software está intentando determinar cuál de los 20 proyectos de software debería llevar a cabo. El VNA (en millones de dólares) contribuido por cada proyecto, así como el capital (en millones de dólares) y el número de programadores necesarios para cada uno de los próximos tres años se proporciona en la hoja de cálculo Modelo básico en el archivo Capbudget.xlsx, que se muestra en la Figura 30-1 en la página siguiente. Por ejemplo, Project 2 produce 908 millones de dólares. Requiere 151 millones de dólares durante el año 1, 269 millones durante el año 2 y 248 millones durante el año 3. Project 2 requiere 139 programadores durante el año 1, 86 programadores durante el año 2 y 83 programadores durante el año 3. Las celdas E4:G4 muestran el capital (en millones de dólares) disponible durante cada uno de los tres años y las celdas H4:J4 indican cuántos programadores están disponibles. Por ejemplo, durante el año 1 hay disponibles hasta 2.500 millones de dólares en capital y 900 programadores.

La empresa debe decidir si debe emprender cada proyecto. Supongamos que no podemos llevar a cabo una fracción de un proyecto de software; si asignamos 0,5 de los recursos necesarios, por ejemplo, tendríamos un programa no laborable que nos traería ingresos de $0.

El truco para modelar situaciones en las que hace o no hace algo es usar celdas con cambios binarios. Una celda binaria que cambia siempre es igual a 0 o 1. Cuando una celda de cambio binario que corresponde a un proyecto es igual a 1, hacemos el proyecto. Si una celda de cambio binario que corresponde a un proyecto es igual a 0, no realizamos el proyecto. Puede configurar Solver para usar un rango de celdas con cambios binarios mediante una restricción: seleccione las celdas cambiantes que desee usar y, después, elija Clase en la lista del cuadro de diálogo Agregar restricción.

Con este fondo, estamos listos para resolver el problema de selección de proyectos de software. Como siempre con un modelo de Solver, comenzamos identificando nuestra celda de destino, las celdas cambiantes y las restricciones.

• Celda de destino. Maximizamos el VNA generado por proyectos seleccionados.

• Cambio de celdas. Se busca una celda de cambio binario 0 o 1 para cada proyecto. He localizado estas celdas en el rango A6:A25 (y he denominado el doit del rango). Por ejemplo, un 1 en la celda A6 indica que emprendemos el Proyecto 1; un 0 en la celda C6 indica que no realizamos el Proyecto 1.

• Restricciones. Tenemos que garantizar que para cada año t (t=1, 2, 3), el capital t año usado es menor o igual que el capital t año disponible y el trabajo t año utilizado es menor o igual que el trabajo t año disponible.

Como puede ver, nuestra hoja de cálculo debe calcular para cualquier selección de proyectos el VNA, el capital usado anualmente y los programadores utilizados cada año. En la celda B2, uso la fórmula SUMAPRODUCTO(doit,VNA) para calcular la VNA total generada por los proyectos seleccionados. (El nombre del rango VNA hace referencia al rango C6:C25). Para cada proyecto con un 1 en la columna A, esta fórmula selecciona el VNA del proyecto y, para cada proyecto con un 0 en la columna A, esta fórmula no selecciona la VNA del proyecto. Por lo tanto, podemos calcular el VNA de todos los proyectos y nuestra celda de destino es lineal porque se calcula sumando los términos que siguen al formulario (cambiar celda)*(constante). De forma similar, calculo el capital usado cada año y la mano de obra usada cada año copiando de E2 a F2:J2 la fórmula SUMAPRODUCTO(doit,E6:E25).

Ahora rellenaré el cuadro de diálogo Parámetros de Solver como se muestra en la figura 30-2.

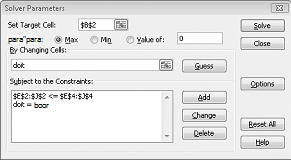
Nuestro objetivo es maximizar VNA de los proyectos seleccionados (celda B2). Nuestras celdas cambiantes (el rango denominado doit) son las celdas binarias cambiantes para cada proyecto. La restricción E2:J2<=E4:J4 garantiza que, durante cada año, el capital y la mano de obra utilizados sean menores o iguales que el capital y la mano de obra disponibles. Para agregar la restricción que hace que el cambio de celdas sea binario, haré clic en Agregar en el cuadro de diálogo Parámetros de Solver y, a continuación, seleccionaré Clase en la lista situada en el medio del cuadro de diálogo. El cuadro de diálogo Agregar restricción debería aparecer como se muestra en la figura 30-3.

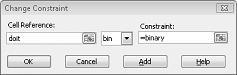
Nuestro modelo es lineal porque la celda de destino se calcula como la suma de términos que tienen el formulario (cambio de celda)*(constante) y porque las restricciones de uso de recursos se calculan comparando la suma de (celdas cambiantes)*(constantes) con una constante.

Con el cuadro de diálogo Parámetros de Solver rellenado, haga clic en Resolver y tenemos los resultados mostrados anteriormente en la figura 30-1. La compañía puede obtener una VNA máxima de 9.293 millones de dólares (9.293 millones de dólares) eligiendo Proyectos 2, 3, 6-10, 14-16, 19 y 20.

A veces, los modelos de selección de proyectos tienen otras restricciones. Por ejemplo, supongamos que si seleccionamos Project 3, también debemos seleccionar Project 4. Dado que nuestra solución óptima actual selecciona Project 3 pero no Project 4, sabemos que nuestra solución actual no puede permanecer óptima. Para solucionar este problema, simplemente agregue la restricción de que la celda de cambio binario de Project 3 sea menor o igual que la celda de cambio binario de Project 4.

Encontrará este ejemplo en la hoja de cálculo Si 3 y 4 del archivo Capbudget.xlsx, que se muestra en la Figura 30-4. Celda L9 hace referencia al valor binario relacionado con Project 3 y la celda L12 al valor binario relacionado con Project 4. Al agregar la restricción L9<=L12, si se elige Project 3, L9 es igual a 1 y la restricción fuerza L12 (el binario de Project 4) para que sea igual a 1. Nuestra restricción también debe dejar el valor binario en la celda cambiante de Project 4 no restringido si no seleccionamos Project 3. Si no seleccionamos Project 3, L9 es igual a 0 y nuestra restricción permite que el binario de Project 4 sea igual a 0 o 1, que es lo que queremos. La nueva solución óptima se muestra en la figura 30-4.

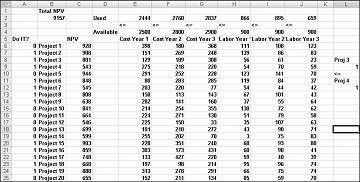
Una nueva solución óptima se calcula si al seleccionar Project 3 significa que también debemos seleccionar Project 4. Ahora supongamos que solo podemos hacer cuatro proyectos de entre los proyectos 1 a 10. (Vea la hoja de cálculo Como máximo 4 de P1–P10 , que se muestra en la figura 30-5). En la celda L8, calculamos la suma de los valores binarios asociados con los proyectos 1 a 10 con la fórmula SUMA(A6:A15). A continuación, agregamos la restricción L8<=L10, lo que garantiza que, como máximo, se seleccionen 4 de los primeros 10 proyectos. La nueva solución óptima se muestra en la figura 30-5. El VNA ha bajado a 9.014.000 millones de dólares.

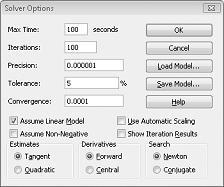
Los modelos de Solver lineales en los que algunas o todas las celdas cambiantes deben ser binarios o enteros suelen ser más difíciles de resolver que los modelos lineales en los que todas las celdas cambiantes pueden ser fracciones. Por esta razón, a menudo estamos satisfechos con una solución casi óptima a un problema de programación binario o entero. Si el modelo de Solver se ejecuta durante mucho tiempo, puede que desee ajustar la configuración de Tolerancia en el cuadro de diálogo Opciones de Solver. (Consulte la figura 30-6). Por ejemplo, un valor de tolerancia del 0,5 % significa que Solver se detendrá la primera vez que encuentre una solución factible que se encuentre dentro del 0,5 por ciento del valor teórico óptimo de la celda objetivo (el valor teórico óptimo de celda objetivo es el valor objetivo óptimo que se encuentra cuando se omiten las restricciones binarias y enteras). A menudo nos encontramos con una opción entre encontrar una respuesta dentro del 10 por ciento de lo óptimo en 10 minutos o encontrar una solución óptima en dos semanas de tiempo de equipo. El valor predeterminado de Tolerancia es 0,05 %, lo que significa que Solver se detiene cuando encuentra un valor de celda Objetivo dentro del 0,05 por ciento del valor teórico óptimo de celda objetivo.

1. Una empresa tiene nueve proyectos en consideración. El VNA agregado por cada proyecto y el capital requerido por cada proyecto durante los próximos dos años se muestra en la tabla siguiente. (Todos los números son millones). Por ejemplo, Project 1 sumará 14 millones de dólares en VNA y requerirá gastos de 12 millones de dólares durante el año 1 y 3 millones durante el año 2. Durante el año 1, se dispone de 50 millones de dólares en capital para proyectos y 20 millones de dólares durante el año 2.

	NPV	Gastos del año 1	Gastos del año 2
Proyecto 1	14	1,2	3
Project 2	17	54	7
Project 3	17	6	6
Proyecto 4	15	6	2
Project 5	40	30	35
Project 6	1,2	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	1,2	18	3

• Si no podemos llevar a cabo una fracción de un proyecto pero debemos llevar a cabo todo o ninguno de un proyecto, ¿cómo podemos maximizar VNA?

• Supongamos que, si se lleva a cabo el Proyecto 4, debe emprenderse el Proyecto 5. ¿Cómo podemos maximizar NPV?

• Una editorial intenta determinar cuál de los 36 libros debería publicar este año. La Pressdata.xlsx de archivos proporciona la siguiente información sobre cada libro:

  • Ingresos proyectados y costos de desarrollo (en miles de dólares)

  • Páginas de cada libro

  • Si el libro está dirigido a una audiencia de desarrolladores de software (indicado por un 1 en la columna E)

    Una empresa editorial puede publicar libros de hasta 8500 páginas este año y debe publicar al menos cuatro libros dirigidos a desarrolladores de software. ¿Cómo puede la empresa maximizar sus beneficios?

Este artículo fue adaptado de Análisis de datos y modelado de negocios de Microsoft Office Excel 2007 por Wayne L. Winston.

Este libro de estilo aula fue desarrollado a partir de una serie de presentaciones de Wayne Winston, un conocido estadístico y profesor de negocios que se especializa en aplicaciones creativas y prácticas de Excel.