Estimates standard deviation based on a sample. The standard deviation is a measure of how widely values are dispersed from the average value (the mean). Text and logical values such as TRUE and FALSE are included in the calculation.
Syntax
STDEVA(value1,value2,...)
Value1,value2,... are 1 to 30 values corresponding to a sample of a population.
Remarks
-
STDEVA assumes that its arguments are a sample of the population. If your data represents the entire population, you must compute the standard deviation using STDEVPA.
-
Arguments that contain TRUE evaluate as 1; arguments that contain text or FALSE evaluate as 0 (zero). If the calculation must not include text or logical values, use the STDEV spreadsheet function instead.
-
The standard deviation is calculated using the "nonbiased" or "n-1" method.
-
STDEVA uses the following formula:
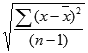
Example
Suppose 10 tools stamped from the same machine during a production run are collected as a random sample and measured for breaking strength.
|
St1 |
St2 |
St3 |
St4 |
St5 |
St6 |
St7 |
St8 |
St9 |
St10 |
Formula |
Description (Result) |
|
1345 |
1301 |
1368 |
1322 |
1310 |
1370 |
1318 |
1350 |
1303 |
1299 |
=STDEVA([St1], [St2], [St3], [St4], [St5], [St6], [St7], [St8], [St9], [St10]) |
Standard deviation of breaking strength for all the tools (27.46391572) |







