En este tema se describen las diferentes opciones de línea de tendencia disponibles en Office.
Use este tipo de línea de tendencia para crear una línea recta de ajuste perfecto para conjuntos de datos lineales simples. Los datos son lineales si el patrón en sus puntos de datos son similares a una línea. Una línea de tendencia lineal frecuentemente muestra que hay algo que aumenta o disminuye a un ritmo constante.
Una línea de tendencia lineal usa esta ecuación para calcular el ajuste de mínimos cuadrados para una línea:
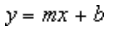
donde m es la pendiente y b es la intersección.
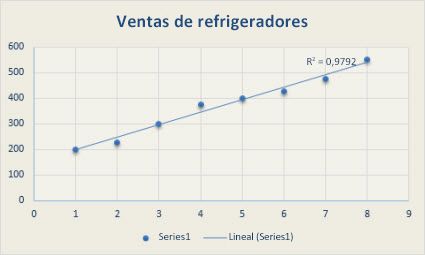
La siguiente línea de tendencia lineal muestra que la venta de refrigeradores ha aumentado de forma regular durante un período de 8 años. Observe que el valor R cuadrado (un número que oscila entre 0 y 1 que revela cuál es la proximidad de correspondencia de los valores estimados para la línea de tendencia con sus datos reales) es 0,9792, lo que representa un buen ajuste de la línea en relación con los datos.
Mostrando una línea curva de ajuste perfecto, esta línea de tendencia es útil cuando la tasa de cambio de los datos aumenta o disminuye rápidamente y luego se nivela. Una línea de tendencia logarítmica puede utilizar valores negativos y positivos.
Una línea de tendencia logarítmica usa esta ecuación que calcula el ajuste de mínimos cuadrados a través de puntos:
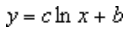
donde c y b son constantes y ln es la función logarítmica natural.
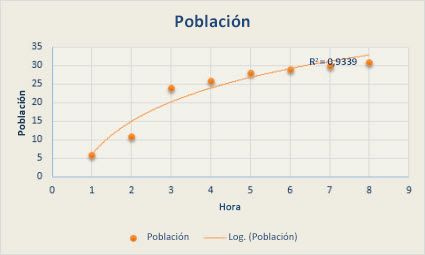
La siguiente línea de tendencia logarítmica muestra el crecimiento previsto en la población animal de un área específica, donde la población se niveló a medida que disminuyó el espacio para los animales. Observe que el valor R cuadrado es 0,933, lo cual representa un buen ajuste de la línea en relación con los datos.
Esta línea de tendencia polinómica es útil cuando hay fluctuaciones de datos. Por ejemplo, al analizar ganancias y pérdidas en un gran conjunto de datos. El orden del polinomio se puede determinar por la cantidad de fluctuaciones en los datos o por la cantidad de ajustes (máximos y mínimos) que aparecen en la curva. Normalmente, una línea de tendencia polinómica de segundo orden solamente posee un máximo o mínimo, una línea de tendencia polinómica de tercer orden posee uno o dos máximos o mínimos y una línea de tendencia de cuarto orden posee hasta tres máximos o mínimos.
Una línea de tendencia polinómica o curvilínea usa esta ecuación para calcular el ajuste de mínimos cuadrados a través de los puntos:
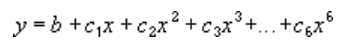
donde b y 
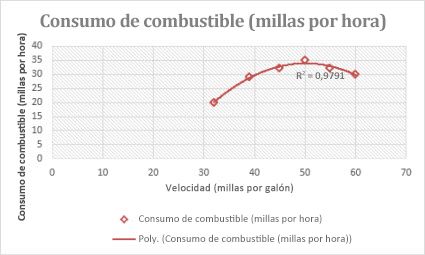
La siguiente línea de tendencia polinómica de segundo orden (un máximo) muestra la relación entre la velocidad y el consumo de combustible. Observe que el valor R cuadrado es 0,979, lo cual se aproxima a 1 de modo que resulta un buen ajuste de la línea en relación con los datos.
Al mostrar una línea curva, esta línea de tendencia es útil para conjuntos de datos que comparan medidas que aumentan a una velocidad específica. Por ejemplo, la aceleración de un coche de carreras a intervalos de 1 segundo. No puede crear una línea de tendencia de potencia si los datos contienen valores negativos o cero.
Una línea de tendencia de potencia usa esta ecuación que calcula el ajuste de mínimos cuadrados a través de los puntos:
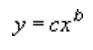
donde c y b son constantes.
Nota: Esta opción no está disponible cuando los datos incluyen valores negativos o cuando no se incluye ningún valor.
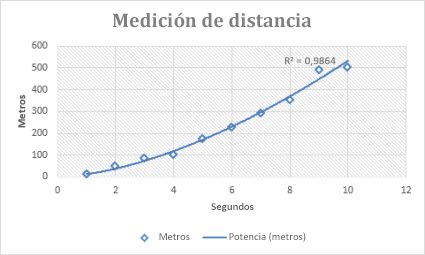
En el siguiente gráfico de medición de distancia se muestra la distancia en metros por segundos. Claramente, la línea de tendencia de potencia demuestra una aceleración en aumento. Observe que el valor R cuadrado es 0,986, lo cual representa un ajuste casi perfecto de la línea en relación con los datos.
Al mostrar una línea curva, esta línea de tendencia es útil cuando los valores de datos suben o bajan según tasas en aumento constante. No se puede crear una línea de tendencia exponencial si los datos contienen valores negativos o si no contienen valores.
Una línea de tendencia exponencial usa esta ecuación para calcular el ajuste de mínimos cuadrados a través de los puntos:
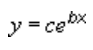
donde c y b son constantes y e es la base del logaritmo natural.
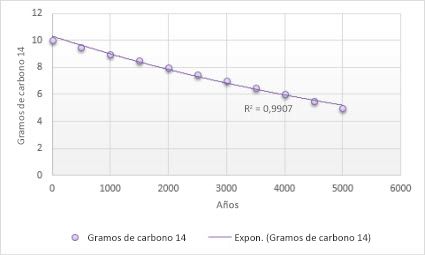
La siguiente línea de tendencia exponencial muestra la cantidad de carbono 14 en disminución en un objeto a medida que pasa el tiempo. Observe que el valor de R cuadrado es 0,990, lo cual significa que la línea se ajusta casi perfectamente a los datos.
Esta línea de tendencia equilibra las fluctuaciones de los datos para mostrar con más claridad un patrón o una tendencia. Una media móvil utiliza una cantidad específica de puntos de datos (establecidos por la opción Período), los promedia y utiliza el valor promedio como un punto en la línea. Por ejemplo, si Período se establece en 2, el promedio de los dos primeros puntos de datos se utiliza como el primer punto en la línea de tendencia de media móvil. El promedio del segundo y tercer punto de datos se utiliza como el segundo punto de la línea de tendencia, etc.
Una línea de tendencia de media móvil usa esta ecuación:
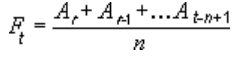
La cantidad de puntos en una línea de tendencia de media móvil equivale a la cantidad total de puntos en la serie menos la cantidad especificada para el período.
En un gráfico de dispersión, la línea de tendencia se basará en el orden de los valores X del gráfico. Para obtener un mejor resultado, ordene los valores X antes de agregar una media móvil.
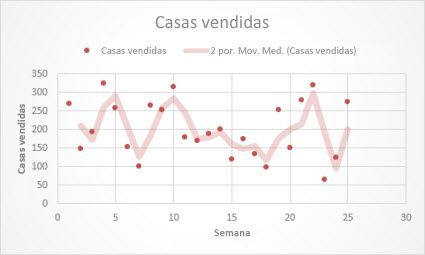
La siguiente línea de tendencia de media móvil muestra un patrón en la cantidad de viviendas que se vendieron en un período de 26 semanas.
Importante: A partir de la versión 2005 de Excel, Excel ajustó la forma en que calcula el valor R2 para las líneas de tendencia lineales en gráficos donde la intersección de la línea de tendencia se establece en cero (0). Este ajuste corrige los cálculos que generaron valores deR2 incorrectos y alinea el cálculo de R2 con la función ESTIMACION.LINEAL. Como resultado, es posible que vea diferentes valores de R2 en gráficos creados anteriormente en versiones anteriores de Excel. Para obtener más información, vea Cambios en los cálculos internos de líneas de tendencia lineales en un gráfico.
¿Necesita más ayuda?
Siempre puede preguntar a un experto en la Excel Tech Community u obtener soporte técnico en Comunidades.
Vea también
Agregar una línea de media móvil o de tendencia a un gráfico







