En este artículo se describen la sintaxis de la fórmula y el uso de la función PENDIENTE en Microsoft Excel.
Descripción
Devuelve la pendiente de una línea de regresión lineal creada con los datos de los argumentos conocido_x y conocido_y. La pendiente es la distancia vertical dividida por la distancia horizontal entre dos puntos cualquiera de la recta, lo que corresponde a la tasa de cambio a lo largo de la línea de regresión.
Sintaxis
PENDIENTE(conocido_y, conocido_x)
La sintaxis de la función PENDIENTE tiene los siguientes argumentos:
-
Conocido_y Obligatorio. Es una matriz o un rango de celdas de puntos de datos numéricos dependientes.
-
Conocido_x Obligatorio. Es el conjunto de puntos de datos independientes.
Observaciones
-
Los argumentos deben ser números o nombres, matrices o referencias que contengan números.
-
Si el argumento de matriz o referencia contiene texto, valores lógicos o celdas vacías, estos valores se ignoran; sin embargo, se incluyen las celdas con el valor cero.
-
Si los argumentos conocido_y y conocido_x están vacíos o contienen un número diferente de puntos de datos, PENDIENTE devuelve el valor de error #N/A.
-
La ecuación para la pendiente de la línea de regresión es la siguiente:
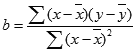
Donde x e y son las medias de muestra PROMEDIO(conocido_x) y PROMEDIO(conocido y).
-
El algoritmo subyacente usado en las funciones PENDIENTE e INTERSECCION.EJE es diferente al algoritmo subyacente usado en la función ESTIMACION.LINEAL. La diferencia entre estos algoritmos puede producir resultados distintos cuando los datos son indeterminados y colineales. Por ejemplo, si los puntos de datos del argumento conocido_y son 0 y los puntos de datos del argumento conocido_x son 1:
-
PENDIENTE e INTERSECCION.EJE devuelven un #DIV/0! #VALOR!. El algoritmo de PENDIENTE e INTERSECCION.EJE está diseñado para buscar una sola respuesta y, en este caso, puede haber más de una respuesta.
-
ESTIMACION.LINEAL devuelve un valor 0. El algoritmo ESTIMACION.LINEAL está diseñado para devolver resultados razonables para los datos colineales y, en este caso, se puede encontrar al menos una respuesta.
-
Ejemplo
Copie los datos de ejemplo en la tabla siguiente y péguelos en la celda A1 de una hoja de cálculo nueva de Excel. Para que las fórmulas muestren los resultados, selecciónelas, presione F2 y luego ENTRAR. Si lo necesita, puede ajustar el ancho de las columnas para ver todos los datos.
|
Datos |
||
|---|---|---|
|
Y conocido |
X conocido |
|
|
1/2/1900 |
6 |
|
|
3/1/1900 |
5 |
|
|
9/1/1900 |
11 |
|
|
1/1/1900 |
7 |
|
|
8/1/1900 |
5 |
|
|
7/1/1900 |
4 |
|
|
5/1/1900 |
4 |
|
|
Fórmula |
Descripción |
Resultado |
|
=PENDIENTE(A3:A9;B3:B9) |
Pendiente de la línea de regresión lineal mediante los puntos de datos en A3:A9 y B3:B9. |
0,305556 |







