Función INTERVALO.CONFIANZA.NORM

Descripción

El intervalo de confianza es un intervalo de valores. La media de la muestra, x está en el centro de este intervalo y el intervalo es x ± INTERVALO.CONFIANZA.NORM. Por ejemplo, si x es la media de una muestra de tiempos de entrega de productos encargados por correo, x ± INTERVALO.CONFIANZA.NORM es un intervalo de medias de la población. Para cualquier media de población µ0 en este intervalo, la probabilidad de obtener una media de muestra más alejada de µ0 que de x es mayor que alfa; para cualquier media de población µ0 fuera del intervalo, la probabilidad de obtener una media de muestra más alejada de µ0 que de x es menor que alfa. Es decir, suponga que usamos x, desv_estándar y tamaño para crear una prueba de dos colas con un nivel de significación alfa de la hipótesis consistente en que la media de la población es μ0. Entonces, no rechazaremos la hipótesis si μ0 está dentro del intervalo de confianza, y la rechazaremos en caso de que μ0 no esté en el intervalo de confianza. El intervalo de confianza no nos permite inferir que hay una probabilidad 1 – alfa de que el tiempo de entrega del próximo paquete que encarguemos estará dentro del intervalo de confianza.

Sintaxis

INTERVALO.CONFIANZA.NORM(alfa;desv_estándar;tamaño)

La sintaxis de la función INTERVALO.CONFIANZA.NORM tiene los siguientes argumentos:

• Alfa     Obligatorio. El nivel de significación usado para calcular el nivel de confianza. El nivel de confianza es igual a 100*(1 - alfa)%, es decir, un alfa de 0,05 indica un nivel de confianza del 95%.

• Desv_estándar     Obligatorio. La desviación estándar de la población para el rango de datos; se presupone que es conocida.

• Tamaño     Obligatorio. El tamaño de la muestra.

Observaciones

• Si uno de los argumentos no es numérico, INTERVALO.CONFIANZA. NORM devuelve el #VALUE. o #VALOR!.

• Si alfa ≤ 0 o alfa ≥ 1, INTERVALO.CONFIANZA. NORM devuelve el #NUM! error #¡NUM!.

• Si standard_dev ≤ 0, INTERVALO.CONFIANZA. NORM devuelve el #NUM! valor de error.

• Si el argumento tamaño no es un entero, se trunca.

• Si el tamaño < 1, INTERVALO.CONFIANZA. NORM devuelve el #NUM! valor de error.

• Si suponemos que el argumento alfa es igual a 0,05, se tendrá que calcular el área debajo de la curva normal estándar que es igual a (1 - alfa) o 95%. Este valor es ± 1,96. Por lo tanto, el intervalo de confianza es:

  

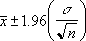
Ejemplo

Copie los datos de ejemplo en la tabla siguiente y péguelos en la celda A1 de una hoja de cálculo nueva de Excel. Para que las fórmulas muestren los resultados, selecciónelas, presione F2 y luego ENTRAR. Si lo necesita, puede ajustar el ancho de las columnas para ver todos los datos.