Calculates standard deviation based on the entire population given as arguments, including text and logical values. The standard deviation is a measure of how widely values are dispersed from the average value (the mean).
Syntax
STDEVPA(value1,value2,...)
Value1,value2,... are 1 to 30 values corresponding to a population.
Remarks
-
STDEVPA assumes that its arguments are the entire population. If your data represents a sample of the population, you must compute the standard deviation using STDEVA.
-
Arguments that contain TRUE evaluate as 1; arguments that contain text or FALSE evaluate as 0 (zero). If the calculation must not include text or logical values, use the STDEVP function instead.
-
For large sample sizes, STDEVA and STDEVPA return approximately equal values.
-
The standard deviation is calculated using the "biased" or "n" method.
-
STDEVPA uses the following formula:
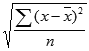
Example
|
St1 |
St2 |
St3 |
St4 |
St5 |
St6 |
St7 |
St8 |
St9 |
St10 |
Formula |
Description (Result) |
|
1345 |
1301 |
1368 |
1322 |
1310 |
1370 |
1318 |
1350 |
1303 |
1299 |
=STDEVPA([St1], [St2], [St3], [St4], [St5], [St6], [St7], [St8], [St9], [St10]) |
Standard deviation of breaking strength, assuming only 10 tools are produced (26.05455814) |