Verwenden von Solver für die Kapitalbudgetierung

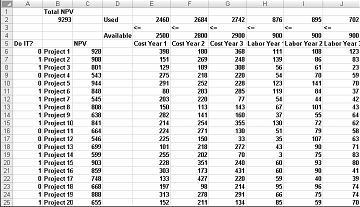
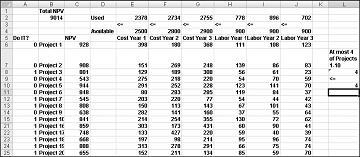
Die meisten Unternehmen möchten Projekte durchführen, die den größten Netto-Barwert (NPV) beitragen, vorbehaltlich begrenzter Ressourcen (in der Regel Kapital und Arbeit). Angenommen, ein Softwareentwicklungsunternehmen versucht zu bestimmen, welches der 20 Softwareprojekte es durchführen sollte. Die von den einzelnen Projekten zur Verfügung gestellten NPV (in Millionen Dollar) sowie das Kapital (in Millionen Dollar) und die Anzahl der Programmierer, die in den nächsten drei Jahren benötigt werden, sind auf dem Arbeitsblatt Basismodell in der Datei Capbudget.xlsx angegeben, die in Abbildung 30-1 auf der nächsten Seite dargestellt ist. Project 2 liefert beispielsweise 908 Millionen US-Dollar. Dies erfordert 151 Millionen US-Dollar im Jahr 1, 269 Millionen US-Dollar im Jahr 2 und 248 Millionen US-Dollar im Jahr 3. Projekt 2 erfordert 139 Programmierer im Jahr 1, 86 Programmierer im Jahr 2 und 83 Programmierer im Jahr 3. Die Zellen E4:G4 zeigen das Kapital (in Millionen Dollar) an, das in jedem der drei Jahre zur Verfügung steht, und die Zellen H4:J4 geben an, wie viele Programmierer verfügbar sind. Im Jahr 1 stehen beispielsweise bis zu 2,5 Milliarden US-Dollar Kapital und 900 Programmierer zur Verfügung.

Das Unternehmen muss entscheiden, ob es jedes Projekt übernehmen soll. Nehmen wir an, dass wir keinen Bruchteil eines Softwareprojekts durchführen können. Wenn wir z. B. 0,5 der benötigten Ressourcen zuordnen, hätten wir ein nicht arbeitsfreies Programm, das uns einen Umsatz von 0 US-Dollar bringen würde!

Der Trick bei der Modellierung von Situationen, in denen Sie etwas tun oder nicht tun, besteht darin, binäre Zellen zu verwenden, die sich ändern. Eine binäre Zelle, die sich ändert, ist immer gleich 0 oder 1. Wenn eine binäre Zelle, die einem Projekt entspricht, gleich 1 ist, wird das Projekt ausgeführt. Wenn eine binäre Zelle, die einem Projekt entspricht, gleich 0 ist, wird das Projekt nicht ausgeführt. Sie richten Solver so ein, dass ein Bereich binärer Zellen verwendet wird, indem Sie eine Einschränkung hinzufügen. Wählen Sie die zu verwendenden veränderbaren Zellen aus, und wählen Sie dann bin aus der Liste im Dialogfeld Einschränkung hinzufügen aus.

Mit diesem Hintergrund sind wir bereit, das Problem der Softwareprojektauswahl zu lösen. Wie immer bei einem Solver-Modell beginnen wir damit, unsere Zielzelle, die sich ändernden Zellen und die Einschränkungen zu identifizieren.

• Zielzelle. Wir maximieren den von ausgewählten Projekten generierten NPV.

• Ändern von Zellen. Wir suchen nach einer 0 oder 1 binären Zelle, die sich für jedes Projekt ändert. Ich habe diese Zellen im Bereich A6:A25 lokalisiert (und den Bereich doit genannt). Beispielsweise gibt eine 1 in Zelle A6 an, dass projekt 1 ausgeführt wird; Eine 0 in Zelle C6 gibt an, dass Projekt 1 nicht ausgeführt wird.

• Zwänge. Wir müssen sicherstellen, dass für jedes Jahr t (t=1, 2, 3) das verwendete Jahreskapital kleiner oder gleich dem verfügbaren Jahres-t-Kapital ist und das jahr t verwendete Arbeit kleiner oder gleich Jahr t arbeit verfügbar ist.

Wie Sie sehen können, muss unser Arbeitsblatt für jede Auswahl von Projekten den NPV, das jährlich verwendete Kapital und die Programmierer berechnen, die jedes Jahr verwendet werden. In Zelle B2 verwende ich die Formel SUMMENPRODUKT(doit,NPV), um den gesamten von ausgewählten Projekten generierten NPV zu berechnen. (Der Bereichsname NPV bezieht sich auf den Bereich C6:C25.) Für jedes Projekt mit einem 1 in Spalte A übernimmt diese Formel den NPV des Projekts, und für jedes Projekt mit einer 0 in Spalte A wird mit dieser Formel nicht der NPV des Projekts erfasst. Daher können wir den NPV aller Projekte berechnen, und unsere Zielzelle ist linear, da sie durch Summierung von Begriffen berechnet wird, die der Form folgen (Ändern der Zelle)*(konstante). Auf ähnliche Weise errechene ich das jährlich verwendete Kapital und die arbeite jedes Jahr, indem ich die Formel SUMPRODUCT(doit,E6:E25) von E2 auf F2:J2 kopiere.

Ich füllen nun das Dialogfeld Solver-Parameter aus, wie in Abbildung 30-2 dargestellt.

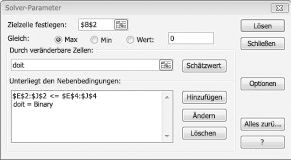
Unser Ziel ist es, den NPV der ausgewählten Projekte (Zelle B2) zu maximieren. Unsere sich ändernden Zellen (der Bereich mit dem Namen doit) sind die binären Zellen, die sich für jedes Projekt ändern. Die Einschränkung E2:J2<=E4:J4 stellt sicher, dass die verwendeten Kapital- und Arbeitsmittel in jedem Jahr kleiner oder gleich dem verfügbaren Kapital und den verfügbaren Arbeitskräften sind. Um die Einschränkung hinzuzufügen, die die sich ändernden Zellen binär macht, klicke ich im Dialogfeld Solver-Parameter auf Hinzufügen und wähle dann in der Liste in der Mitte des Dialogfelds Bin aus. Das Dialogfeld Einschränkung hinzufügen sollte wie in Abbildung 30-3 dargestellt angezeigt werden.

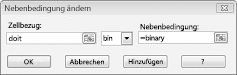
Unser Modell ist linear, da die Zielzelle als Summe von Begriffen berechnet wird, die die Form (ändernde Zelle)*(konstante) haben, und weil die Ressourcennutzungseinschränkungen berechnet werden, indem die Summe von (sich ändernden Zellen)*(Konstanten) mit einer Konstante verglichen wird.

Wenn das Dialogfeld Solver-Parameter ausgefüllt ist, klicken Sie auf Lösen, und es werden die weiter oben in Abbildung 30-1 gezeigten Ergebnisse angezeigt. Das Unternehmen kann einen maximalen Kapitalwert von 9.293 Millionen US-Dollar (9,293 Milliarden US-Dollar) erhalten, indem es projekte 2, 3, 6–10, 14–16, 19 und 20 auswählt.

Manchmal weisen Projektauswahlmodelle andere Einschränkungen auf. Angenommen, wenn wir Projekt 3 auswählen, müssen wir auch Projekt 4 auswählen. Da unsere aktuelle optimale Lösung Projekt 3, aber nicht Projekt 4 auswählt, wissen wir, dass unsere aktuelle Projektmappe nicht optimal bleiben kann. Um dieses Problem zu beheben, fügen Sie einfach die Einschränkung hinzu, dass die binäre Zelle für Projekt 3 kleiner oder gleich der binären Zelle für Project 4 ist.

Sie finden dieses Beispiel auf dem Arbeitsblatt Wenn 3 und dann 4 in der Datei Capbudget.xlsx, die in Abbildung 30-4 dargestellt ist. Zelle L9 bezieht sich auf den Binärwert im Zusammenhang mit Project 3 und Zelle L12 auf den Binärwert im Zusammenhang mit Project 4. Durch Hinzufügen der Einschränkung L9<=L12 entspricht L9, wenn wir Projekt 3 auswählen, L9 gleich 1, und unsere Einschränkung erzwingt L12 (die Project 4-Binärdatei) auf 1. Unsere Einschränkung muss auch den Binärwert in der sich ändernden Zelle von Project 4 unbeschränkt lassen, wenn wir projekt 3 nicht auswählen. Wenn wir Projekt 3 nicht auswählen, ist L9 gleich 0, und die Einschränkung erlaubt es der Projekt 4-Binärdatei, gleich 0 oder 1 zu sein, was wir wollen. Die neue optimale Lösung ist in Abbildung 30-4 dargestellt.

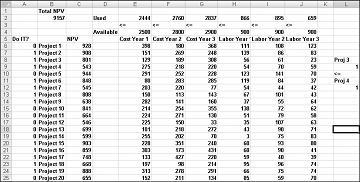
Eine neue optimale Projektmappe wird berechnet, wenn die Auswahl von Projekt 3 bedeutet, dass wir auch Projekt 4 auswählen müssen. Angenommen, wir können nur vier Projekte aus den Projekten 1 bis 10 ausführen. (Siehe das Arbeitsblatt "Höchstens 4 von P1–P10 ", dargestellt in Abbildung 30-5.) In Zelle L8 berechnen wir die Summe der binären Werte, die projekten 1 bis 10 zugeordnet sind, mit der Formel SUMME(A6:A15). Anschließend fügen wir die Einschränkung L8<=L10 hinzu, die sicherstellt, dass höchstens 4 der ersten 10 Projekte ausgewählt werden. Die neue optimale Lösung ist in Abbildung 30-5 dargestellt. Der NPV ist auf 9,014 Milliarden US-Dollar gesunken.

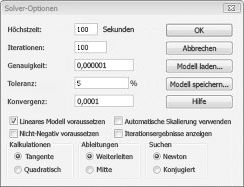
Lineare Solver-Modelle, bei denen einige oder alle sich ändernden Zellen binär oder ganzzahlige Zellen sein müssen, sind in der Regel schwieriger zu lösen als lineare Modelle, bei denen alle sich ändernden Zellen Brüche sein dürfen. Aus diesem Grund sind wir oft mit einer nahezu optimalen Lösung für ein Binäres oder ganzzahliges Programmierproblem zufrieden. Wenn Ihr Solver-Modell lange ausgeführt wird, sollten Sie die Einstellung Toleranz im Dialogfeld Solver-Optionen anpassen. (Siehe Abbildung 30-6.) Eine Toleranzeinstellung von 0,5 % bedeutet beispielsweise, dass Solver beim ersten Mal eine praktikable Lösung findet, die innerhalb von 0,5 Prozent des theoretischen optimalen Zielzellenwerts liegt (der theoretische optimale Zielzellenwert ist der optimale Zielzellenwert, der gefunden wird, wenn die binären und ganzzahligen Einschränkungen weggelassen werden). Oft stehen wir vor der Wahl, eine Antwort innerhalb von 10 Prozent der optimalen in 10 Minuten zu finden oder eine optimale Lösung in zwei Wochen Computerzeit zu finden! Der Standardmäßige Toleranzwert ist 0,05 %. Dies bedeutet, dass Solver anhält, wenn ein Zielzellenwert innerhalb von 0,05 Prozent des theoretischen optimalen Zielzellenwerts gefunden wird.

1. Ein Unternehmen hat neun Projekte in Betracht gezogen. Der von jedem Projekt hinzugefügte NPV und das für jedes Projekt in den nächsten zwei Jahren erforderliche Kapital sind in der folgenden Tabelle dargestellt. (Alle Zahlen sind in Millionen angegeben.) Beispielsweise wird Project 1 14 Millionen US-Dollar an NPV hinzufügen und erfordert Ausgaben von 12 Millionen US-Dollar im Jahr 1 und 3 Millionen US-Dollar im Jahr 2. Im Jahr 1 stehen 50 Millionen US-Dollar Kapital für Projekte zur Verfügung, und 20 Millionen US-Dollar stehen im Jahr 2 zur Verfügung.

	NBW	Ausgaben für Jahr 1	Ausgaben für Jahr 2
Projekt 1	14	12	3
Projekt 2	17	54	7
Projekt 3	17	6	6
Projekt 4	15	6	2
Projekt 5	40	30	35
Projekt 6	12	6	6
Projekt 7	14	48	4
Projekt 8	10	36	3
Projekt 9	12	18	3

• Wie können wir dann den NPV maximieren, wenn wir keinen Teil eines Projekts durchführen können, aber entweder alle oder keines projektieren müssen?

• Angenommen, wenn Projekt 4 durchgeführt wird, muss Projekt 5 durchgeführt werden. Wie können wir NPV maximieren?

• Ein Verlag versucht zu bestimmen, welches von 36 Büchern er in diesem Jahr veröffentlichen soll. Die Datei Pressdata.xlsx enthält die folgenden Informationen zu jedem Buch:

  • Prognostizierte Einnahmen und Entwicklungskosten (in Tausend Dollar)

  • Seiten in jedem Buch

  • Ob das Buch an eine Zielgruppe von Softwareentwicklern ausgerichtet ist (angegeben durch eine 1 in Spalte E)

    Ein Verlag kann in diesem Jahr Bücher mit insgesamt bis zu 8500 Seiten veröffentlichen und muss mindestens vier Bücher für Softwareentwickler veröffentlichen. Wie kann das Unternehmen seinen Gewinn maximieren?

Dieser Artikel wurde von Microsoft Office Excel 2007 Data Analysis and Business Modeling von Wayne L. Winston angepasst.

Dieses Buch im Unterrichtsstil wurde aus einer Reihe von Präsentationen von Wayne Winston entwickelt, einem bekannten Statistiker und Wirtschaftsprofessor, der sich auf kreative, praktische Anwendungen von Excel spezialisiert hat.