In diesem Artikel werden die Formelsyntax und die Verwendung der Funktion NEGBINOM.VERT in Microsoft Excel beschrieben.
Beschreibung
Gibt Wahrscheinlichkeiten einer negativen, binominal verteilten Zufallsvariablen zurück. NEGBINOM.VERT berechnet, wie wahrscheinlich es ist, dass es "Zahl_Mißerfolge" vor dem durch "Zahl_Erfolge" angegebenen Erfolg gibt, wobei "Erfolgswahrsch" die Wahrscheinlichkeit für den günstigen Ausgang des Experiments ist.
Die Vorgehensweise dieser Funktion unterscheidet sich von der Binomialverteilung nur dadurch, dass die Anzahl der Erfolge feststeht und die Anzahl der Versuche variabel ist. Analog zu einer Binomialverteilung wird vorausgesetzt, dass die jeweiligen Versuche voneinander unabhängig sind.
Zum Beispiel sollen Sie 5 Personen ausfindig machen, die hervorragende Reflexe haben, und Sie wissen, dass die Wahrscheinlichkeit, dass ein Kandidat diese Forderung erfüllt, 0,25 ist. NEGBINOM.VERT berechnet die Wahrscheinlichkeit, mit der Sie eine bestimmte Anzahl nicht geeigneter Kandidaten befragen, bevor Sie 5 geeignete Kandidaten ausfindig gemacht haben.
Syntax
NEGBINOM.VERT(Zahl_Mißerfolge;Zahl_Erfolge;Erfolgswahrsch;Kumuliert)
Die Syntax der Funktion NEGBINOM.VERT weist die folgenden Argumente auf:
-
Zahl_Mißerfolge Erforderlich. Die Zahl der ungünstigen Ereignisse
-
Zahl_Erfolge Erforderlich. Die Zahl der günstigen Ereignisse
-
Erfolgswahrsch Erforderlich. Die Wahrscheinlichkeit für den günstigen Ausgang des Experiments
-
Kumuliert Erforderlich. Ein logischer Wert, der die Form der Funktion bestimmt. Wenn kumulativ TRUE ist, NEGBINOM. DIST gibt die kumulierte Verteilungsfunktion zurück. Wenn FALSE, wird die Wahrscheinlichkeitsdichtefunktion zurückgegeben.
Hinweise
-
"Zahl_Mißerfolge" und "Zahl_Erfolge" werden durch Abschneiden ihrer Nachkommastellen in ganze Zahlen überführt.
-
Ist eines der Argumente kein numerischer Ausdruck, gibt NEGBINOM.VERT den Fehlerwert #WERT! zurück.
-
Ist Erfolgswahrsch < 0, oder ist Erfolgswahrsch > 1, gibt NEGBINOM.VERT den Fehlerwert #ZAHL! zurück.
-
Ist "Zahl_Mißerfolge" < 0 oder "Zahl_Erfolge" < 1, gibt, NEGBINOM.VERT den Fehlerwert #ZAHL! zurück.
-
Die Gleichung einer negativen Binomialverteilung lautet:
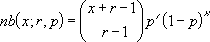
wobei:
x ist gleich "Zahl_Mißerfolge", r ist gleich "Zahl_Erfolge", und p ist gleich "Erfolgswahrsch".
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten |
Beschreibung |
|
|
10 |
Anzahl der Misserfolge |
|
|
5 |
Mindestanzahl der Erfolge |
|
|
0,25 |
Wahrscheinlichkeit für einen Erfolg |
|
|
Formel |
Beschreibung |
Ergebnis |
|
=NEGBINOM.VERT(A2;A3;A4;WAHR) |
Die kumulierte negative binomiale Verteilung für die o. a. Bedingungen |
0,3135141 |
|
=NEGBINOM.VERT(A2;A3;A4;FALSCH) |
Die negative binomiale Wahrscheinlichkeitsverteilung für die o. a. Bedingungen |
0,0550487 |










