In diesem Artikel wird die Verwendung von Solver beschrieben, einem Microsoft Excel-Add-in-Programm, das Sie für was-wäre-wenn-Analysen verwenden können, um einen optimalen Produktmix zu ermitteln.
Wie kann ich den monatlichen Produktmix ermitteln, der die Rentabilität maximiert?
Unternehmen müssen häufig die Menge jedes Produkts ermitteln, das monatlich produziert werden soll. In der einfachsten Form umfasst das Problem der Produktzusammenstellung , wie Sie die Menge jedes Produkts ermitteln, das während eines Monats produziert werden soll, um die Gewinne zu maximieren. Product Mix muss in der Regel die folgenden Einschränkungen beachten:
-
Product Mix kann nicht mehr Ressourcen verwenden, als verfügbar sind.
-
Für jedes Produkt ist eine begrenzte Nachfrage vorhanden. Wir können nicht mehr eines Produkts in einem Monat produzieren, als es die Nachfrage diktiert, weil die überschüssige Produktion verschwendet wird (beispielsweise ein verderbliches Medikament).
Lassen Sie uns nun das folgende Beispiel für das Problem der Produktzusammenstellung lösen. Sie finden die Lösung für dieses Problem in der Datei Prodmix.xlsx, wie in Abbildung 27-1 zu sehen ist.
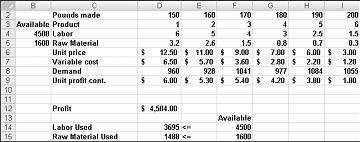
Angenommen, wir arbeiten für ein Pharmaunternehmen, das in seinem Werk sechs verschiedene Produkte produziert. Die Produktion jedes Produkts erfordert Arbeit und Rohmaterial. Zeile 4 in Abbildung 27-1 zeigt die Arbeitszeiten, die erforderlich sind, um ein Pfund pro Produkt zu produzieren, und Zeile 5 zeigt die Pfunde des Rohmaterials, das für die Herstellung eines Pfunds jedes Produkts benötigt wird. Wenn Sie beispielsweise ein Pfund Produkt 1 herstellen, benötigen Sie sechs Arbeitsstunden und 3,2 Pfund Rohmaterial. Für jedes Medikament wird der Preis pro Pfund in Zeile 6 angegeben, die Einheitskosten pro Pfund werden in Zeile 7 angegeben, und der Gewinnbeitrag pro Pfund wird in Zeile 9 angegeben. Beispielsweise verkauft Produkt 2 für $11,00 pro Pfund, einen Einstandspreis von $5,70 pro Pfund und trägt $5,30 Gewinn pro Pfund bei. Der monatliche Bedarf für jedes Medikament ist in Zeile 8 angegeben. Beispielsweise ist die Nachfrage nach Produkt 3 £ 1041. In diesem Monat stehen 4500 Arbeitsstunden und 1600 Pfund Rohmaterial zur Verfügung. Wie kann dieses Unternehmen seinen monatlichen Profit maximieren?
Wenn wir nichts über Excel Solver wussten, würden wir dieses Problem angreifen, indem wir ein Arbeitsblatt erstellen, um die Gewinn-und Ressourcennutzung zu überwachen, die dem Produktmix zugeordnet ist. Dann würden wir Versuchs-und Fehlermeldungen verwenden, um den Produktmix zu variieren, um den Profit zu optimieren, ohne mehr Arbeit oder Rohmaterial zu verwenden, als verfügbar ist, und ohne eine Droge zu produzieren, die die Nachfrage übersteigt. In diesem Prozess verwenden wir Solver nur bei der Test-und Fehler Phase. Solver ist im Grunde ein Optimierungsmodul, das die Test-und Fehlersuche problemlos durchführt.
Ein Schlüssel zur Lösung des Problems der Produktzusammenstellung ist die effiziente Berechnung der Ressourcennutzung und des Gewinns, die mit einem bestimmten Produktmix verbunden sind. Ein wichtiges Tool, mit dem wir diese Berechnung vornehmen können, ist die SumProduct-Funktion. Die SumProduct-Funktion multipliziert die entsprechenden Werte in Zellbereichen und gibt die Summe dieser Werte zurück. Jeder Zellbereich, der in einer SumProduct-Auswertung verwendet wird, muss die gleichen Dimensionen aufweisen, was impliziert, dass Sie SumProduct mit zwei Zeilen oder zwei Spalten verwenden können, jedoch nicht mit einer Spalte und einer Zeile.
Als Beispiel, wie wir die SumProduct-Funktion in unserem Beispiel für die Produktzusammenstellung verwenden können, versuchen wir, unsere Ressourcennutzung zu berechnen. Unsere Arbeits Nutzung wird berechnet durch
(Arbeitsaufwand pro Kilogramm Droge 1) * (produzierte Droge 1 Pfund) + (Arbeitsaufwand pro Kilogramm Droge 2) * (produzierte Droge 2 Pfund) +. .. (Arbeitsaufwand pro Kilogramm Droge 6) * (produzierte Droge 6 Pfund)
Wir können den Arbeits Verbrauch auf eine langwierigere Weise als D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * R4berechnen. Ebenso könnte die Verwendung von Rohmaterial als D2 * D5 + E2 *E5 + F2 * F5 + G2 * G5 + H2 * H5 + I2 * I5berechnet werden. Die Eingabe dieser Formeln in ein Arbeitsblatt für sechs Produkte ist allerdings zeitaufwändig. Stellen Sie sich vor, wie lange es dauern würde, wenn Sie mit einem Unternehmen zusammenarbeiten, das beispielsweise 50-Produkte in seinem Werk produziert hat. Eine viel einfachere Möglichkeit zum Berechnen von Arbeits-und Rohmaterial Nutzung besteht darin, die Formel SumProduct ($D $2: $I $2, D4: R4)von D14 in D15 zu kopieren. Diese Formel berechnet D2 * D4 + E2 * E4 + F2 * F4 + G2 * G4 + H2 * H4 + I2 * R4 (was unsere Arbeits Nutzung ist), ist aber viel einfacher einzugeben! Beachten Sie, dass ich das $-Zeichen mit dem Bereich D2: I2 verwende, damit ich, wenn ich die Formel kopiee, die Produktmischung aus Zeile 2 noch erfassen kann. Die Formel in der Zelle D15 berechnet die Verwendung des Rohmaterials.
Auf ähnliche Weise wird unser Gewinn durch
(Medikament 1 Profit pro Pfund) * (produzierte Droge 1 Pfund) + (Arzneimittel 2 Gewinn pro Pfund) * (produzierte Droge 2 Pfund) +. .. (Medikament 6 Gewinn pro Pfund) * (produzierte Droge 6 Pfund)
Der Gewinn wird in Zelle D12 einfach mit der Formel SumProduct (D9: i9, $D $2: $I $2)berechnet.
Wir können nun die drei Komponenten unseres Product Mix Solver-Modells identifizieren.
-
Zielzelle Unser Ziel ist es, den Profit zu maximieren (berechnet in Zelle D12).
-
Ändern von Zellen Die Anzahl der pro Produkt produzierten Pfunde (im Zellbereich D2: I2 aufgeführt)
-
Einschränkungen. Wir haben die folgenden Einschränkungen:
-
Verwenden Sie nicht mehr Arbeit oder Rohmaterial, als verfügbar ist. Das bedeutet, dass die Werte in den Zellen D14: D15 (die verwendeten Ressourcen) kleiner oder gleich den Werten in den Zellen F14: F15 (die verfügbaren Ressourcen) sein müssen.
-
Produzieren Sie nicht mehr als eine Droge, die gefragt ist. Das bedeutet, dass die Werte in den Zellen D2: I2 (Pounds, die für jedes Medikament produziert werden) kleiner oder gleich dem Bedarf für jedes Medikament sein müssen (in Zellen D8: I8 aufgeführt).
-
Wir können keine negativen Mengen an Medikamenten produzieren.
-
Ich werde Ihnen zeigen, wie Sie die Zielzelle eingeben, Zellen und Abhängigkeiten in Solver ändern. Dann müssen Sie einfach auf die Schaltfläche "lösen" klicken, um einen Produkt-Mix zu finden, der Profit maximiert.
Klicken Sie zunächst auf die Registerkarte Daten, und klicken Sie dann in der Gruppe Analyse auf Solver.
Hinweis: Wie in Kapitel 26, "Einführung in die Optimierung mit Excel-Solver" erläutert, wird Solver installiert, indem Sie auf die Microsoft Office-Schaltfläche und dann auf Excel-Optionen und anschließend auf Add-Ins klicken. Klicken Sie in der Liste verwalten auf Excel-Add-Ins, aktivieren Sie das Kontrollkästchen Solver-Add-in, und klicken Sie dann auf OK.
Das Dialogfeld Solver-Parameter wird angezeigt, wie in Abbildung 27-2 dargestellt.
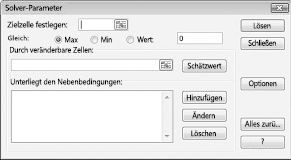
Klicken Sie auf das Feld Ziel Zelle festlegen, und wählen Sie dann unsere Gewinn Zelle (Zelle D12) aus. Klicken Sie auf das Feld durch Ändern der Zellen, und zeigen Sie dann auf den Bereich D2: I2, in dem die von den einzelnen Medikamenten produzierten Pfunde enthalten sind. Das Dialogfeld sollte nun Abbildung 27-3 aussehen.
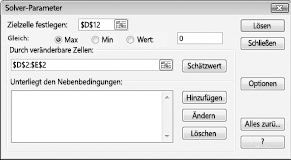
Wir sind nun bereit, dem Modell Einschränkungen hinzuzufügen. Klicken Sie auf die Schaltfläche hinzufügen. Das Dialogfeld "Einschränkung hinzufügen" wird in Abbildung 27-4 angezeigt.
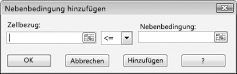
Klicken Sie zum Hinzufügen der Einschränkungen für die Ressourcennutzung auf das Feld Zellbezug, und wählen Sie dann den Bereich D14: D15 aus. Wählen Sie <= aus der mittleren Liste aus. Klicken Sie auf das Feld Einschränkung, und wählen Sie dann den Zellbereich F14: F15 aus. Das Dialogfeld "Einschränkung hinzufügen" sollte nun wie in Abbildung 27-5 aussehen.
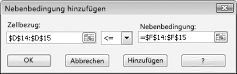
Wir haben nun sichergestellt, dass beim Solver verschiedene Werte für die sich verändernden Zellen verwendet werden, nur Kombinationen, die sowohl D14<= F14 (Arbeitsaufwand ist kleiner als oder gleich der verfügbaren Arbeit) entsprechen, und D15<= F15 (das verwendete Rohmaterial ist kleiner als oder gleich dem verfügbaren Rohstoff) wird berücksichtigt. Klicken Sie auf Hinzufügen, um die Bedarfs Einschränkungen einzugeben. Füllen Sie das Dialogfeld Einschränkung hinzufügen aus, wie in Abbildung 27-6 dargestellt.
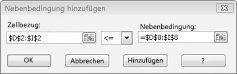
Durch Hinzufügen dieser Einschränkungen wird sichergestellt, dass beim Solver verschiedene Kombinationen für die sich ändernden Zellwerte verwendet werden, nur Kombinationen berücksichtigt werden, die die folgenden Parameter erfüllen:
-
D2<= D8 (der Betrag, der von Droge 1 erzeugt wird, ist kleiner oder gleich dem Bedarf für Droge 1)
-
E2<= E8 (die Menge der produzierten Droge 2 ist kleiner oder gleich der Nachfrage nach Droge 2)
-
F2<= F8 (der Betrag, der von Droge 3 hergestellt wird, ist kleiner als oder gleich dem Bedarf für Droge 3)
-
G2<= G8 (der Betrag, der von Droge 4 hergestellt wird, ist kleiner oder gleich der Nachfrage nach Droge 4)
-
H2<= h8 (der Betrag, der von Droge 5 hergestellt wird, ist kleiner oder gleich der Nachfrage nach Droge 5)
-
I2<= I8 (der Betrag, der von Droge 6 hergestellt wird, ist kleiner oder gleich der Nachfrage nach Droge 6)
Klicken Sie im Dialogfeld Einschränkung hinzufügen auf OK. Das Solver-Fenster sollte wie in Abbildung 27-7 aussehen.
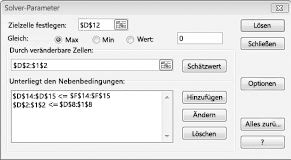
Wir geben die Einschränkung ein, dass das Ändern von Zellen im Dialogfeld Solver-Optionen nicht negativ sein muss. Klicken Sie im Dialogfeld Solver-Parameter auf die Schaltfläche Optionen. Aktivieren Sie das Kontrollkästchen Lineares Modell voraussetzen und das Kontrollkästchen nicht negativ annehmen, wie in Abbildung 27-8 auf der nächsten Seite dargestellt. Klicken Sie auf "OK".
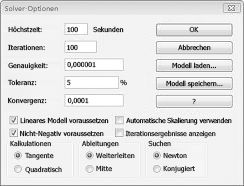
Durch Aktivieren des Felds nicht negativ annehmen wird sichergestellt, dass Solver nur Kombinationen aus sich ändernden Zellen berücksichtigt, bei denen jede veränderbare Zelle einen nicht negativen Wert annimmt. Wir haben das Kontrollkästchen Lineares Modell annehmen überprüft, da es sich bei dem Problem der Produktzusammenstellung um einen speziellen Solver-Problemtyp handelt, der als Lineares Modellbezeichnet wird. Im Grunde ist ein Solver-Modell unter den folgenden Bedingungen linear:
-
Die Zielzelle wird berechnet, indem die Ausdrücke des Formulars (veränderbare Zelle) * (Konstante)addiert werden.
-
Jede Einschränkung erfüllt die "lineare Modell Anforderung". Dies bedeutet, dass jede Einschränkung ausgewertet wird, indem die Ausdrücke des Formulars (veränderbare Zelle) * (Konstante) addiert und die Summen mit einer Konstante verglichen werden.
Warum ist dieses Solver-Problem linear? Die Ziel Zelle (Profit) wird berechnet als
(Medikament 1 Profit pro Pfund) * (produzierte Droge 1 Pfund) + (Arzneimittel 2 Gewinn pro Pfund) * (produzierte Droge 2 Pfund) +. .. (Medikament 6 Gewinn pro Pfund) * (produzierte Droge 6 Pfund)
Diese Berechnung folgt einem Muster, in dem der Wert der Zielzelle abgeleitet wird, indem die Ausdrücke des Formulars (veränderbare Zelle) * (Konstante)addiert werden.
Unser Arbeitszwang wird ausgewertet, indem der Wert von (Arbeit pro Kilogramm Droge 1) * (produzierte Droge 1 Pfund) + (Arbeitsaufwand pro Kilogramm Droge 2) * (die Droge, die 2 pounds produziert hat) + verglichen wird... (Arbeit unsEd pro Pfund Droge 6) * (produzierte Droge 6 Pfund) zur verfügbaren Arbeit.
Aus diesem Grund wird die Einschränkung "Arbeit" ausgewertet, indem die Ausdrücke des Formulars (veränderbare Zelle) * (Konstante) addiert und die Summen mit einer Konstante verglichen werden. Sowohl die Einschränkung "Arbeit" als auch die Rohstoffabhängigkeit erfüllen die lineare Modell Anforderung.
Unsere nach Frage Einschränkungen übernehmen das Formular
(Droge 1 produziert) <= (Droge 1-Nachfrage) (Arzneimittel 2 produziert) <= (Arzneimittel 2-Nachfrage) § (Medikament 6 produziert) <= (Droge 6-Nachfrage)
Jede Anforderungs Einschränkung erfüllt auch die Anforderung für das lineare Modell, da jeder ausgewertet wird, indem die Ausdrücke des Formulars (veränderbare Zelle) * (Konstante) addiert und die Summen mit einer Konstante verglichen werden.
Nachdem wir gezeigt haben, dass unser Produktmix ein lineares Modell ist, warum sollten wir uns darum kümmern?
-
Wenn ein Solver-Modell linear ist und wir lineares Modell annehmen auswählen, wird Solver garantiert die optimale Lösung für das Solver-Modell finden. Wenn ein Solver-Modell nicht linear ist, kann Solver möglicherweise die optimale Lösung finden.
-
Wenn ein Solver-Modell linear ist und wir lineares Modell annehmen auswählen, verwendet Solver einen sehr effizienten Algorithmus (die Simplex-Methode), um die optimale Lösung für das Modell zu finden. Wenn ein Solver-Modell linear ist und wir das lineare Modell nicht annehmen auswählen, verwendet Solver einen sehr ineffizienten Algorithmus (die GRG2-Methode) und hat möglicherweise Schwierigkeiten, die optimale Lösung für das Modell zu finden.
Nachdem Sie im Dialogfeld Solver-Optionen auf OK geklickt haben, kehren wir zum Dialogfeld Haupt Solver zurück, das weiter oben in Abbildung 27-7 angezeigt wird. Wenn wir auf "lösen" klicken, berechnet Solver eine optimale Lösung (sofern vorhanden) für unser Produktmix-Modell. Wie ich in Kapitel 26 dargelegt habe, wäre eine optimale Lösung für das Product Mix-Modell eine Reihe veränderlicher Zellwerte (Pounds der einzelnen Arzneimittel), die den Gewinn über die Menge aller machbaren Lösungen maximieren. Eine realisierbare Lösung besteht wiederum in einer Reihe von sich ändernden Zellwerten, die alle Einschränkungen erfüllen. Die in Abbildung 27-9 gezeigten veränderlichen Zellwerte sind eine realisierbare Lösung, da alle Produktionsebenen nicht negativ sind, Produktionsebenen den Bedarf nicht überschreiten und die Ressourcennutzung die verfügbaren Ressourcen nicht überschreitet.
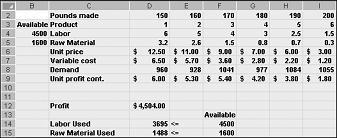
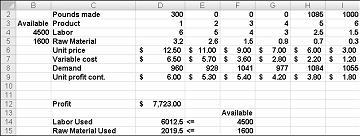
Die in Abbildung 27-10 auf der nächsten Seite gezeigten Werte für das Ändern von Zellen stellen eine nicht realisierbare Lösung aus den folgenden Gründen dar:
-
Wir produzieren mehr von Droge 5 als die Nachfrage dafür.
-
Wir nutzen mehr Arbeit als das, was verfügbar ist.
-
Wir verwenden mehr Rohmaterial als das, was verfügbar ist.
Nachdem Sie auf solve geklickt haben, findet Solver schnell die optimale Lösung, die in Abbildung 27-11 gezeigt wird. Sie müssen Solver-Lösung beibehalten auswählen, um die optimalen Lösungswerte auf dem Arbeitsblatt beizubehalten.
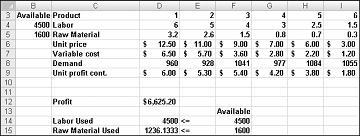
Unser Arzneimittel-Unternehmen kann seinen monatlichen Profit auf einem Niveau von $6.625,20 maximieren, indem es 596,67 Pfund Droge 4, 1084 Pfund Droge 5 produziert, und keiner der anderen Drogen! Wir können nicht feststellen, ob der Höchstgewinn von $6.625,20 auf andere Weise erreicht werden kann. Wir können sicher sein, dass es mit unseren limitierten Ressourcen und der Nachfrage keine Möglichkeit gibt, mehr als $6.627,20 in diesem Monat zu erzielen.
Nehmen wir an, dass die Nachfrage für jedes Produkt erfüllt sein muss . (Weitere Informationen finden Sie im Arbeitsblatt " keine realisierbare Lösung " in der Datei Prodmix.xlsx.) Wir müssen dann unsere Anforderungseinschränkungen von d2: I2<= D8: I8 zu d2: I2>= D8: I8ändern. Öffnen Sie dazu Solver, wählen Sie die Einschränkung D2: I2<= D8: I8 aus, und klicken Sie dann auf ändern. Das Dialogfeld "Einschränkung ändern" (siehe Abbildung 27-12) wird angezeigt.
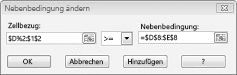
Wählen Sie >= aus, und klicken Sie dann auf OK. Wir haben nun sichergestellt, dass Solver die Änderung nur von Zellwerten in Frage stellt, die allen Anforderungen entsprechen. Wenn Sie auf "lösen" klicken, wird die Meldung "Solver konnte keine realisierbare Lösung finden" angezeigt. Diese Meldung bedeutet nicht, dass wir in unserem Modell einen Fehler gemacht haben, sondern dass wir mit unseren limitierten Ressourcen die Nachfrage für alle Produkte nicht erfüllen können. Solver sagt uns einfach, dass wir, wenn wir die Nachfrage für jedes Produkt befriedigen möchten, mehr Arbeit, mehr Rohstoffe oder mehr von beiden hinzufügen müssen.
Schauen wir uns an, was passiert, wenn wir eine unbegrenzte Nachfrage für jedes Produkt zulassen und wir zulassen, dass für jedes Medikament negative Mengen produziert werden. (Dieses Solver-Problem wird im Datei Prodmix.xlsx auf dem Arbeitsblatt festgelegte Werte nicht konvergieren angezeigt.) Um die optimale Lösung für diese Situation zu finden, öffnen Sie Solver, klicken Sie auf die Schaltfläche Optionen, und deaktivieren Sie das Kontrollkästchen nicht negativ annehmen. Wählen Sie im Dialogfeld Solver-Parameter die Anforderungs Einschränkung D2: I2<= D8: I8 aus, und klicken Sie dann auf löschen, um die Einschränkung zu entfernen. Wenn Sie auf "lösen" klicken, gibt Solver die Meldung "Zellwerte werden nicht konvergieren" zurück. Diese Meldung bedeutet Folgendes: Wenn die Zielzelle maximiert werden soll (wie in unserem Beispiel), gibt es realisierbare Lösungen mit beliebig hohen Zielzellen Werten. (Wenn die Zielzelle minimiert werden soll, bedeutet die Meldung "Zellenwerte nicht konvergieren", dass es machbare Lösungen mit willkürlich kleinen Zielzellen Werten gibt.) In unserer Situation, indem wir eine negative Produktion einer Droge zulassen, schaffen wir in der Tat Ressourcen, die dazu verwendet werden können, willkürlich große Mengen anderer Drogen zu produzieren. Angesichts unserer unbegrenzten Nachfrage können wir dadurch unbegrenzte Gewinne erzielen. In einer wirklichen Situation können wir keine unendlich viel Geld verdienen. Kurz gesagt: Wenn "festgelegte Werte nicht konvergieren" angezeigt wird, hat Ihr Modell einen Fehler.
-
Angenommen, unser Arzneimittelunternehmen kann bis zu 500 Arbeitsstunden bei $1 mehr pro Stunde als die aktuellen Arbeitskosten erwerben. Wie können wir den Profit maximieren?
-
Bei einem Chip-Fertigungswerk produzieren vier Techniker (a, B, C und D) drei Produkte (Produkte 1, 2 und 3). In diesem Monat kann der Chiphersteller 80 Einheiten des Produkts 1, 50 Einheiten von Produkt 2 und höchstens 50 Einheiten des Produkts 3 verkaufen. Techniker A kann nur Produkte 1 und 3 herstellen. Techniker B kann nur Produkte 1 und 2 erstellen. Der Techniker C kann nur Produkt 3 erstellen. Techniker D kann nur Produkt 2 erstellen. Für jede produzierte Einheit tragen die Produkte folgenden Profit bei: Produkt 1, $6; Produkt 2, $7; und Produkt 3, $10. Die Zeit (in Stunden), die jeder Techniker für die Herstellung eines Produkts benötigt, lautet wie folgt:
Produkt
Techniker A
Techniker B
Techniker C
Techniker D
1
2
2,5
Nicht möglich
Nicht möglich
2
Nicht möglich
3
Nicht möglich
3,5
3
3
Nicht möglich
4
Nicht möglich
-
Jeder Techniker kann bis zu 120 Stunden pro Monat arbeiten. Wie kann der Chiphersteller seinen monatlichen Gewinn maximieren? Nehmen Sie an, dass eine gebrochene Anzahl von Einheiten produziert werden kann.
-
Eine Computer Fabrik produziert Mäuse, Keyboards und Joysticks für Videospiele. Der pro-Einheit-Profit, pro-Einheit-Auslastung, monatlicher Bedarf und pro-Einheit-Maschinenzeit Verbrauch sind in der folgenden Tabelle angegeben:
Mäuse
Keyboards
Joysticks
Profit/Einheit
$8
$11
$9
Arbeitsauslastung/-Einheit
.2 Stunde
.3 Stunde
.24 Stunden
Maschinenzeit/-Einheit
.04 Stunde
.055 Stunde
.04 Stunde
Monatliche Nachfrage
15.000
27.000
11.000
-
Pro Monat stehen insgesamt 13.000 Arbeitsstunden und 3000 Stunden Maschinenzeit zur Verfügung. Wie kann der Hersteller seinen monatlichen Gewinnbeitrag aus der Anlage maximieren?
-
Lösen Sie unser Arzneimittel Beispiel aus, vorausgesetzt, dass für jedes Medikament eine mindestnachfrage von 200 Einheiten erfüllt sein muss.
-
Jason macht Diamanten Armbänder, Halsketten und Ohrringe. Er möchte maximal 160 Stunden pro Monat arbeiten. Er hat 800 Unzen Diamanten. Die Gewinne, Arbeitszeiten und Unzen von Diamanten, die für die Herstellung jedes Produkts benötigt werden, sind unten angegeben. Wie kann Jason seinen Profit maximieren, wenn die Nachfrage für jedes Produkt unbegrenzt ist?
Produkt
Einheits Gewinn
Arbeitsstunden pro Einheit
Unzen Diamanten pro Einheit
Armband
300 €
.35
1,2
Halskette
200 €
.15
.75
Ohrringe
100 €
.05
0,5










