I denne artikel beskrives formelsyntaksen for og brugen af funktionen ULIGE.SIDSTE.AFKAST i Microsoft Excel.
Beskrivelse
Returnerer afkastet for et værdipapir med ulige (kort eller lang) sidste periode.
Syntaks
ULIGE.SIDSTE.AFKAST(afregningsdato;udløbsdato;sidste_rente;rente;kurs;indløsningskurs;hyppighed;[datotype])
Vigtigt!: Datoer skal angives ved hjælp af funktionen DATO eller som resultater af andre formler eller funktioner. Brug f.eks. DATO(2008;5;23) for den 23. maj 2008. Der kan opstå problemer, hvis datoer skrives som tekst.
Syntaksen for funktionen ULIGE.SIDSTE.AFKAST har følgende argumenter:
-
Afregningsdato Påkrævet. Værdipapirets afregningsdato. Værdipapirets afregningsdato er den dato efter udstedelsesdatoen, hvor værdipapiret overdrages til køber.
-
Udløbsdato Påkrævet. Værdipapirets udløbsdato. Udløbsdatoen er den dato, hvor værdipapiret udløber.
-
Sidste_rente Påkrævet. Værdipapirets sidste kupondato.
-
Rente Påkrævet. Værdipapirets rente.
-
Kurs Påkrævet. Værdipapirets kurs.
-
Indløsningskurs Påkrævet. Værdipapirets indløsningskurs pr. kr. 100 nominel værdi.
-
Hyppighed Påkrævet. Antallet af kuponudbetalinger pr. år. Ved årlige udbetalinger er hyppighed = 1, ved halvårlige udbetalinger er hyppighed = 2, og ved kvartalsvise udbetalinger er hyppighed = 4.
-
Datotype Valgfrit. Datotypen, der skal anvendes.
|
Datotype |
Antal dage |
|---|---|
|
0 eller udeladt |
US (NASD) 30/360 |
|
1 |
Faktisk/faktisk |
|
2 |
Faktisk/360 |
|
3 |
Faktisk/365 |
|
4 |
Europæisk 30/360 |
Bemærkninger
-
Microsoft Excel lagrer datoer som sekventielle serienumre, så de kan bruges i beregninger. Som standard har 1. januar 1900 serienummer 1, og 1. januar 2008 har serienummer 39448, fordi datoen falder 39.448 dage efter den 1. januar 1900.
-
Afregningsdatoen er den dato, hvor køber erhverver en kupon, f.eks. en obligation. Udløbsdatoen er den dato, hvor en kupon udløber. Antag f.eks., at en 30-års obligation udstedes 1. januar 2008 og købes af en køber seks måneder senere. Udstedelsesdatoen ville være 1. januar 2008, afregningsdatoen være 1. juli 2008 og udløbsdatoen være 1. januar 2038, hvilket er 30 år efter 1. januar 2008, udstedelsesdatoen.
-
Afregningsdato, udløbsdato, sidste_rente og datotype afkortes til heltal.
-
Hvis afregningsdato, udløbsdato eller last_interest ikke er en gyldig dato, returnerer ULIGE.SIDSTE.AFKAST #VALUE! fejlværdi.
-
Hvis rente < 0, eller hvis kurs ≤ 0, returnerer ULIGE.SIDSTE.AFKAST #NUM! fejlværdi.
-
Hvis datotype < 0, eller hvis datotype > 4, returnerer ULIGE.SIDSTE.AFKAST #NUM! fejlværdi.
-
Følgende betingelse for dato skal være opfyldt: Ellers returnerer ULIGE.SIDSTE.AFKAST #NUM! som fejlværdi:
udløbsdato > afregningsdato > sidste_rente
-
ULIGE.SIDSTE.AFKAST beregnes således:
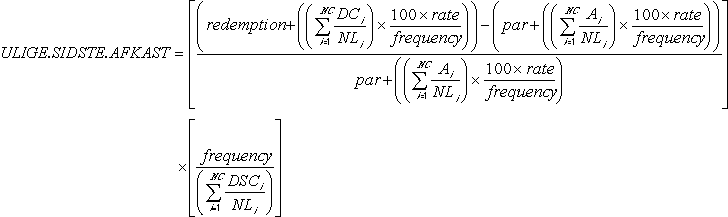
hvor:
-
Pi = antallet af påløbne dage for den iende eller sidste kvasi-kuponperiode i ulige periode. Der tælles fremad fra sidste rentetilskrivningsdato før indløsning.
-
DKi = antallet af talte dage i hver iende eller sidste kvasi-kuponperiode. Antallet af dage bestemmes af længden af den pågældende kuponperiode.
-
AK = antallet af kvasi-kuponperioder, der går op i ulige periode. Hvis dette tal indeholder en brøk, rundes det op til det nærmeste hele tal.
-
NLi = den iende eller sidste kvasi-kuponperiodes normale længde i dage i ulige kuponperiode.
-
Eksempel
Kopiér eksempeldataene i følgende tabel, og sæt dem ind i celle A1 i et nyt Excel-regneark. For at få formlerne til at vise resultater skal du markere dem, trykke på F2 og derefter trykke på Enter. Hvis der er brug for det, kan du justere bredden på kolonnerne, så du kan se alle dataene.
|
Data |
Beskrivelse af argument |
|
|---|---|---|
|
20-04-2008 |
Afregningsdato |
|
|
15-06-2008 |
Udløbsdato |
|
|
24-12-2007 |
Rentetilskrivningsdato |
|
|
3,75 % |
Kuponrente |
|
|
DKK 99,875 |
Pris |
|
|
DKK 100 |
Indløsningskurs |
|
|
2 |
Frekvens er halvårligt |
|
|
0 |
30/360 datotype |
|
|
Formel |
Beskrivelse |
Resultat |
|
=ULIGE.SIDSTE.AFKAST(A2; A3; A4; A5; A6; A7; A8; A9) |
Afkastet for et værdipapir med en ulige (kort eller lang) sidste periode for obligationen med brug af betingelserne i cellerne A2:A10 som funktionsargumenter. Resultatet er 0,04519 eller 4,52 %. |
4,52 % |










