Indstillinger for tendenslinje i Office

Brug denne type tendenslinje til at oprette en ret linje til enkle, lineære datasæt. Dataene er lineære, hvis mønsteret i dets datapunkter ser ud som en linje. En lineær tendenslinje angiver normalt, at noget er stadigt stigende eller faldende.

En lineær tendenslinje bruger denne ligning til at beregne tilpasningen af de mindste kvadrater for en linje:

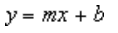
hvor m er hældningen, og b er skæringen.

Den følgende lineære tendenslinje viser, at salget af køleskabe er steget konsekvent over en periode på 8 år. Bemærk, at den R-kvadrerede værdi (et tal fra 0 til 1, som viser, hvor nært de estimerede værdier for tendenslinjen svarer til dine faktiske data) er 0,979, hvilket viser, at linjen passer godt til dataene.

Denne tendenslinje, der viser den bedst tilpassede kurve, er nyttig, når hastigheden af ændringer i dataene øges eller reduceres hurtigt og derefter udjævnes. I en logaritmisk tendenslinje kan der bruges negative og positive værdier.

En lineær tendenslinje anvender denne ligning, der beregner tilpasningen af de mindste kvadrater gennem punkter:

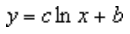
hvor c og b er konstanter, og ln er den naturlige logaritmefunktion.

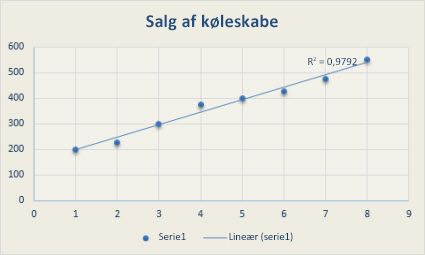
Følgende logaritmiske tendenslinje viser en forventet vækst i bestanden af dyr med en bestemt mængde plads, hvor bestanden udjævnede sig, efterhånden som pladsen til dyrene blev mindre. Bemærk, at den R-kvadrerede værdi er 0,933, hvilket viser, at linjen passer relativt godt til dataene.

Denne tendenslinje er nyttig, når dine data svinger. Når du f.eks. analyserer gevinster og tab over et stort datasæt. Polynomiens rækkefølge kan bestemmes af antallet af udsving i dataene eller af, hvor mange bøjninger (bakker og dale) der vises i kurven. Typisk har en polynomisk tendenslinje i Order 2 kun én bakke eller dal, en Ordre 3 har en eller to bakker eller dale, og en Ordre 4 har op til tre bakker eller dale.

En polynomisk eller buet tendenslinje ved hjælp af følgende ligning, der beregner tilpasningen af de mindste kvadrater gennem punkter:

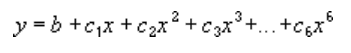
hvor b og er konstanter.

Følgende polynomiske tendenslinje i rækkefølge 2 (én bakke) viser forholdet mellem kørehastighed og brændstofforbrug. Bemærk, at den R-kvadrerede værdi er 0,979, hvilket er tæt på 1, så linjen passer godt til dataene.

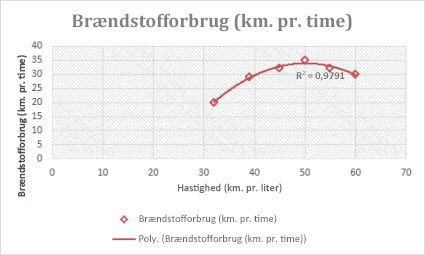
Denne tendenslinje, der viser en kurvet linje, er nyttig til datasæt, der sammenligner de målinger, der forøges med et bestemt interval, f.eks. en racerbils acceleration med et-sekundsintervaller. Du kan ikke oprette en potenstendenslinje, hvis dataene indeholder nulværdier eller negative værdier.

En potenstendenslinje bruger denne ligning, der beregner tilpasningen af de mindste kvadrater gennem punkter:

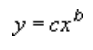
hvor c og b er konstanter.

Følgende afstandsmålingsdiagram viser afstand i meter gange sekunder. Potenslinjen viser klart den stigende acceleration. Bemærk, at den R-kvadrerede værdi er 0,986, hvilket betyder, at linjen passer næsten perfekt til dataene.

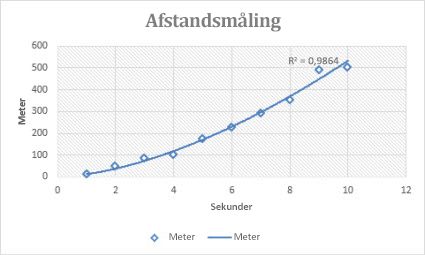
Denne tendenslinje viser en kurve, der er meget praktisk, når dataværdier stiger eller falder i konstant større intervaller. Du kan ikke oprette en eksponentiel tendenslinje, hvis dine data indeholder nulværdier eller negative værdier.

En eksponentiel tendenslinje ved hjælp af følgende ligning, der beregner tilpasningen af de mindste kvadrater gennem punkter:

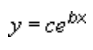
hvor c og b er konstanter, og e er logaritmens grundtal.

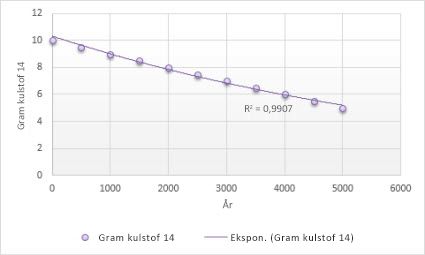
Den følgende eksponentielle tendenslinje viser den faldende mængde af kulstof 14 i et objekt, efterhånden som det bliver ældre. Bemærk, at den R-kvadrerede værdi er 0,990, hvilket betyder, at linjen passer næsten perfekt til dataene.

Denne tendenslinje udjævner udsving i data for at vise et mønster eller en tendens mere tydeligt. Et glidende gennemsnit bruger et bestemt antal datapunkter (angivet med indstillingen Periode ), beregner gennemsnittet af dem og bruger gennemsnitsværdien som et punkt på linjen. Hvis Periode f.eks. er angivet til 2, bruges gennemsnittet af de første to datapunkter som det første punkt i tendenslinjen med glidende gennemsnit. Gennemsnittet af det andet og tredje datapunkt bruges som det andet punkt i tendenslinjen osv.

En tendenslinje med glidende gennemsnit bruger følgende ligning:

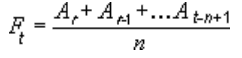
Antallet af punkter i en tendenslinje for et bevægeligt gennemsnit er lig med det samlede antal punkter i en serie minus det antal, du angiver for perioden.

I et punktdiagram er tendenslinjen baseret på rækkefølgen af x-værdier i diagrammet. Du kan opnå et bedre resultat ved at sortere x-værdierne, før du tilføjer et glidende gennemsnit.

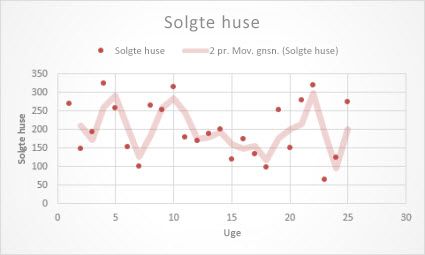
Følgende glidende gennemsnitstendenslinje viser et mønster for antallet af boliger solgt over en periode på 26 uger.