Brug af Problemløser til kapitalbudgettering

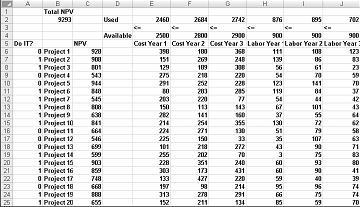
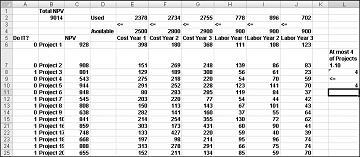
De fleste virksomheder ønsker at gennemføre projekter, der bidrager med den største nettonutidsværdi (NUTIDSVÆRDI), underlagt begrænsede ressourcer (normalt kapital og arbejdskraft). Lad os sige, at en softwareudviklingsvirksomhed forsøger at afgøre, hvilke af 20 softwareprojekter den skal gennemføre. NPV (i millioner af dollars) bidraget af hvert projekt samt kapitalen (i millioner af dollars) og antallet af programmører, der er nødvendige i løbet af hvert af de næste tre år, er angivet i regnearket Basismodel i filen Capbudget.xlsx, som er vist i figur 30-1 på næste side. Project 2 giver f.eks. 908 millioner dollars. Det kræver $ 151 millioner i år 1, $ 269 millioner i løbet af år 2, og $ 248 millioner i år 3. Projekt 2 kræver 139 programmører i år 1, 86 programmører i år 2, og 83 programmører i år 3. Cellerne E4:G4 viser den tilgængelige kapital (i millioner af dollars) i løbet af hvert af de tre år, og cellerne H4:J4 angiver, hvor mange programmører der er tilgængelige. For eksempel er der i år 1 op til $ 2,5 milliarder i kapital og 900 programmører tilgængelige.

Virksomheden skal beslutte, om den skal gennemføre hvert projekt. Lad os antage, at vi ikke kan foretage en brøkdel af et softwareprojekt; hvis vi tildeler 0,5 af de nødvendige ressourcer, for eksempel, ville vi have en nonworking program, der ville bringe os $ 0 omsætning!

Tricket i modelleringssituationer, hvor du enten gør eller ikke gør noget, er at bruge binære skiftende celler. En binær ændringscelle er altid lig med 0 eller 1. Når en binær ændringscelle, der svarer til et projekt, er lig med 1, udfører vi projektet. Hvis en binær ændringscelle, der svarer til et projekt, er lig med 0, udfører vi ikke projektet. Du konfigurerer Problemløser til at bruge et område af binære skiftende celler ved at tilføje en begrænsning – markér de celler, der ændrer, du vil bruge, og vælg derefter Bin på listen i dialogboksen Tilføj begrænsning.

Med denne baggrund er vi klar til at løse problemet med valg af softwareprojekt. Som altid med en Problemløser-model begynder vi med at identificere vores målcelle, de skiftende celler og begrænsningerne.

• Målcelle. Vi maksimerer den NUTIDSVÆRDI, der genereres af udvalgte projekter.

• Ændring af celler. Vi søger efter en binær ændringscelle på 0 eller 1 for hvert projekt. Jeg har fundet disse celler i området A6:A25 (og navngivet området doit). Et 1 i celle A6 angiver f.eks., at vi påtager os Project 1. Et 0 i celle C6 angiver, at vi ikke påtager os Project 1.

• Begrænsninger. Vi er nødt til at sikre, at for hvert år t (t=1, 2, 3), år t-kapital , der bruges, er mindre end eller lig med Tilgængelig year t-kapital , og År t arbejdskraft brugt er mindre end eller lig med Tilgængelig år t-arbejdskraft .

Som du kan se, skal vores regneark beregne for enhver udvælgelse af projekter NPV, den kapital, der anvendes årligt, og de programmører, der anvendes hvert år. I celle B2 bruger jeg formlen SUMPRODUKT(doit,NUTIDSVÆRDI) til at beregne den samlede NUTIDSVÆRDI, der genereres af udvalgte projekter. Områdenavnet NUTIDSVÆRDI refererer til området C6:C25. For hvert projekt med 1 i kolonne A henter denne formel projektets NUTIDSVÆRDI, og for hvert projekt med 0 i kolonne A opfanger denne formel ikke NUTIDSVÆRDI for projektet. Derfor kan vi beregne NUTIDSVÆRDI for alle projekter, og vores målcelle er lineær, fordi den beregnes ved at opsummere ord, der følger formularen (ændringscelle)*(konstant). På samme måde beregner jeg den anvendte kapital hvert år, og arbejdskraften bruges hvert år ved at kopiere formlen SUMPRODUKT(doit,E6:E25)fra E2 til F2:J2.

Jeg udfylder nu dialogboksen Parametre til Problemløser som vist i Figur 30-2.

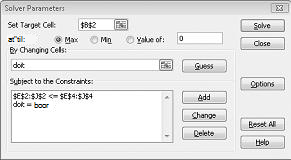
Vores mål er at maksimere NUTIDSVÆRDI for udvalgte projekter (celle B2). Vores skiftende celler (området kaldet doit) er de binære skiftende celler for hvert projekt. Betingelsen E2:J2<=E4:J4 sikrer, at den anvendte kapital og arbejdskraft i løbet af hvert år er mindre end eller lig med den tilgængelige kapital og arbejdskraft. Hvis jeg vil tilføje den begrænsning, der gør de skiftende celler binære, klikker jeg på Tilføj i dialogboksen Parametre til Problemløser og vælger derefter Bin på listen midt i dialogboksen. Dialogboksen Tilføj begrænsning vises som vist i Figur 30-3.

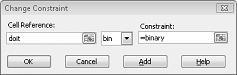
Vores model er lineær, fordi målcellen beregnes som summen af udtryk, der har formularen (skiftende celle)*(konstant), og fordi begrænsningerne for ressourceforbrug beregnes ved at sammenligne summen af (skiftende celler)*(konstanter) med en konstant.

Når dialogboksen Parametre til Problemløser er udfyldt, skal du klikke på Løs, og vi har vist resultaterne tidligere i Figur 30-1. Virksomheden kan opnå en maksimal NPV på $ 9.293 millioner ($ 9.293 milliarder) ved at vælge Projekter 2, 3, 6-10, 14-16, 19 og 20.

Nogle gange har projektudvælgelsesmodeller andre begrænsninger. Antag f.eks., at hvis vi vælger Projekt 3, skal vi også vælge Projekt 4. Da vores nuværende optimale løsning vælger Project 3, men ikke Project 4, ved vi, at vores nuværende løsning ikke kan forblive optimal. For at løse dette problem skal du blot tilføje den begrænsning, at den binære ændringscelle for Project 3 er mindre end eller lig med den binære ændringscelle for Project 4.

Du kan finde dette eksempel i regnearket Hvis 3 og 4 i filen Capbudget.xlsx, som er vist i figur 30-4. Celle L9 refererer til den binære værdi, der er relateret til Project 3, og celle L12 til den binære værdi, der er relateret til Project 4. Ved at tilføje begrænsningen L9<=L12, og hvis vi vælger Project 3, er L9 lig med 1, og vores begrænsning tvinger L12 (binær project 4) til at svare til 1. Vores begrænsning skal også lade den binære værdi i den ændrede celle i Project 4 være ubegrænset, hvis vi ikke vælger Project 3. Hvis vi ikke vælger Project 3, er L9 lig med 0, og vores begrænsning tillader, at binær Project 4 er lig med 0 eller 1, hvilket er det, vi ønsker. Den nye optimale løsning er vist i figur 30-4.

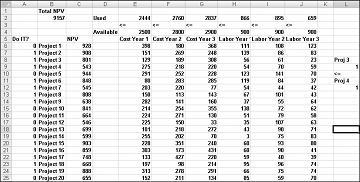
Der beregnes en ny optimal løsning, hvis du vælger Project 3, så vi også skal vælge Projekt 4. Antag nu, at vi kun kan udføre fire projekter mellem Projekter 1 til 10. Se regnearket Højst 4 af P1-P10 , der er vist i figur 30-5. I celle L8 beregner vi summen af de binære værdier, der er knyttet til Projekter 1 til 10 med formlen SUM(A6:A15). Derefter tilføjer vi begrænsningen L8<=L10, hvilket sikrer, at højst 4 af de første 10 projekter vælges. Den nye optimale løsning er vist i figur 30-5. NUTIDSVÆRDI er faldet til 9,014 mia.

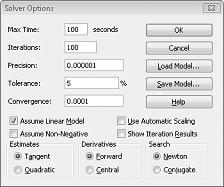
Lineære Problemløser-modeller, hvor nogle eller alle skiftende celler skal være binære eller heltal, er normalt sværere at løse end lineære modeller, hvor alle skiftende celler har tilladelse til at være brøker. Derfor er vi ofte tilfredse med en næsten optimal løsning på et binært eller heltals programmeringsproblem. Hvis din Problemløser-model kører i lang tid, kan du overveje at justere toleranceindstillingen i dialogboksen Indstillinger for Problemløser. (Se figur 30-6). En toleranceindstilling på 0,5 % betyder f.eks., at Problemløser stopper, første gang der findes en mulig løsning, der ligger inden for 0,5 % af den teoretiske optimale målcelleværdi (den teoretiske optimale målcelleværdi er den optimale målværdi, der findes, når de binære begrænsninger og heltalsbegrænsninger udelades). Ofte står vi over for et valg mellem at finde et svar inden for 10 procent af det optimale på 10 minutter eller at finde en optimal løsning om to ugers computertid! Standardværdien Tolerance er 0,05 %, hvilket betyder, at Problemløser stopper, når den finder en målcelleværdi inden for 0,05 procent af den teoretiske optimale målcelleværdi.

1. En virksomhed har ni projekter under overvejelse. Den NUTIDSVÆRDI, der lægges til hvert projekt, og den kapital, der kræves for hvert projekt i løbet af de næste to år, er vist i følgende tabel. (Alle tal er i millioner.) Projekt 1 tilføjer f.eks. $14 millioner i NUTIDSVÆRDI og kræver udgifter på $ 12 millioner i år 1 og $ 3 millioner i år 2. I løbet af år 1, er $ 50 millioner i kapital til rådighed for projekter, og $ 20 millioner er til rådighed i løbet af år 2.

	NUTIDSVÆRDI	År 1 udgifter	Udgifter for år 2
Projekt 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Projekt 4	15	6	2
Projekt 5	40	30	35
Projekt 6	12	6	6
Projekt 7	14	48	4
Projekt 8	10	36	3
Projekt 9	12	18	3

• Hvis vi ikke kan udføre en brøkdel af et projekt, men skal gennemføre enten hele eller intet af et projekt, hvordan kan vi så maksimere NUTIDSVÆRDI?

• Antag, at hvis projekt 4 gennemføres, skal Projekt 5 gennemføres. Hvordan kan vi maksimere NUTIDSVÆRDI?

• Et forlag forsøger at afgøre, hvilke af 36 bøger det skal udgive i år. Filen Pressdata.xlsx indeholder følgende oplysninger om hver bog:

  • Forventede indtægter og udviklingsomkostninger (i tusindvis af dollars)

  • Sider i hver bog

  • Om bogen er rettet mod et publikum af softwareudviklere (angivet med en 1 i kolonne E)

    Et forlag kan publicere bøger på i alt op til 8.500 sider i år og skal udgive mindst fire bøger, der er rettet mod softwareudviklere. Hvordan kan virksomheden maksimere sin fortjeneste?

Denne artikel er tilpasset fra Microsoft Office Excel 2007 Data Analysis and Business Modeling af Wayne L. Winston.

Denne klasseværelsesstil bog blev udviklet ud fra en række præsentationer af Wayne Winston, en velkendt statistiker og forretningsprofessor, der har specialiseret sig i kreative, praktiske anvendelser af Excel.