Tento článek popisuje syntaxi vzorce a použití funkce ZTEST v Microsoft Excelu.
Vrátí jednostrannou hodnotu pravděpodobnosti z-testu. Pro danou hypotetickou střední hodnotu základního souboru μ0 vrátí funkce ZTEST pravděpodobnost, že střední hodnota výběru je větší než průměr pozorování v sadě dat (poli), tj. pozorovaná střední hodnota výběru.
Informace o použití funkce ZTEST ve vzorcích pro výpočet oboustranné pravděpodobnostní hodnoty naleznete v níže uvedené části Komentář.
Důležité informace: Tato funkce byla nahrazena jednou či více novými funkcemi, které mohou poskytovat vyšší přesnost a jejichž názvy lépe odpovídají jejich použití. I když je tato funkce stále k dispozici kvůli zpětné kompatibilitě, měli byste dále používat nové funkce, v budoucích verzích aplikace Excel totiž tato funkce již nemusí být k dispozici.
Další informace o nové funkci naleznete v článku Z.TEST (funkce).
Syntaxe
ZTEST(matice,x,[sigma])
Syntaxe funkce ZTEST má následující argumenty:
-
Matice: Povinný argument. Jedná se o matici nebo oblast dat, proti které je testována hodnota x.
-
X: Povinný argument. Jedná se o hodnotu, kterou chcete testovat.
-
Sigma: Nepovinný argument. Jedná se o známou směrodatnou odchylku základního souboru. Pokud není zadána, je použita směrodatná odchylka výběru.
Poznámky
-
Pokud je argument matice prázdný, vrátí funkce ZTEST chybovou hodnotu #NENÍ_K_DISPOZICI.
-
Pokud je zadána hodnota sigma, je funkce ZTEST definována následujícím vztahem:
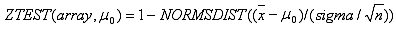
Pokud není hodnota sigma zadána, je definována následujícím vztahem:
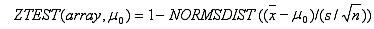
kde x je střední hodnota výběru PRŮMĚR(pole), s je směrodatná odchylka výběru SMODCH.VÝBĚR(pole) a n je počet pozorování ve výběru POČET(pole).
-
Funkce ZTEST určuje pravděpodobnost, že je střední hodnota výběru větší než pozorovaná hodnota PRŮMĚR(pole), pokud je střední hodnota základního souboru μ0. Ze symetrie normálního rozdělení vyplývá, že pokud PRŮMĚR(pole) < μ0, vrátí funkce ZTEST hodnotu větší než 0,5.
-
Pomocí následujícího vzorce aplikace Excel lze vypočítat oboustrannou pravděpodobnost, že je střední hodnota výběru dále od μ0 (v obou směrech) než PRŮMĚR(pole), pokud je střední hodnota základního souboru μ0:
=2×MIN(ZTEST(pole;μ0;sigma);1-ZTEST(pole;μ0;sigma)).
Příklad
Zkopírujte vzorová data v následující tabulce a vložte je do buňky A1 nového excelového sešitu. Aby vzorce zobrazily výsledky, vyberte je, stiskněte F2 a potom stiskněte Enter. Pokud potřebujete, můžete přizpůsobit šířky sloupců a zobrazit si všechna data.
|
Data |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Vzorec |
Popis (výsledek) |
Výsledek |
|
=ZTEST(A2:A11,4) |
Jednostranná hodnota pravděpodobnosti, která je výsledkem z-testu pro výše uvedenou množinu dat při hypotetické střední hodnotě základního souboru 4 (0,090574) |
0,090574 |
|
=2*MIN(ZTEST(A2:A11;4);1-ZTEST(A2:A11;4)) |
Oboustranná hodnota pravděpodobnosti, která je výsledkem z-testu pro výše uvedenou množinu dat při hypotetické střední hodnotě základního souboru 4 (0,181148) |
0,181148 |
|
=ZTEST(A2:A11;6) |
Jednostranná hodnota pravděpodobnosti, která je výsledkem z-testu pro výše uvedenou množinu dat při hypotetické střední hodnotě základního souboru 6 (0,863043) |
0,863043 |
|
=2*MIN(ZTEST(A2:A11;6);1-ZTEST(A2:A11;6)) |
Oboustranná hodnota pravděpodobnosti, která je výsledkem z-testu pro výše uvedenou množinu dat při hypotetické střední hodnotě základního souboru 6 (0,273913) |
0,273913 |










