Použití Řešitele pro rozpočtování kapitálu

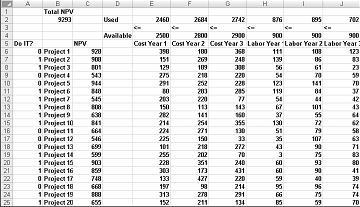
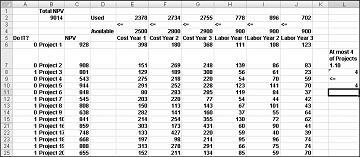
Většina společností chce provádět projekty, které přispívají největší čistou současnou hodnotou (NPV) s omezenými zdroji (obvykle kapitálem a prací). Řekněme, že společnost, která vyvíjí software, se snaží určit, který z 20 softwarových projektů by měla provést. Hodnota NPV (v milionech dolarů) jednotlivými projekty, kapitál (v milionech dolarů) a počet programátorů potřebných během každého z následujících tří let je uveden na listu Základní model v souboru Capbudget.xlsx, který je znázorněn na obrázku 30-1 na další stránce. Například Projekt 2 vynáší 908 milionů USD. Vyžaduje 151 milionů USD během 1. roku, 269 milionů usd během 2. roku a 248 milionů usd během 3. roku. Projekt 2 vyžaduje 139 programátorů během 1. ročníku, 86 programátorů během 2. ročníku a 83 programátorů během 3. ročníku. Buňky E4:G4 zobrazují kapitál (v milionech dolarů) dostupný během každého ze tří let a buňky H4:J4 označují, kolik programátorů je k dispozici. Například během 1. roku je k dispozici až 2,5 miliardy dolarů v kapitálu a 900 programátorů.

Společnost se musí rozhodnout, zda má provést každý projekt. Předpokládejme, že nemůžeme provést zlomek softwarového projektu; Pokud například přidělíme 0,5 potřebných prostředků, budeme mít nepracovní program, který by nám přinesl 0 USD výnosy!

Trik v situacích modelování, ve kterých buď něco děláte nebo neděláte, je použití binárních buněk. Binární změna buňky se vždy rovná 0 nebo 1. Pokud se binární změna buňky, která odpovídá projektu, rovná 1, provedeme projekt. Pokud se binární změna buňky, která odpovídá projektu, rovná 0, projekt neuděláme. Nastavili jste Řešitel tak, aby používal oblast binárních změn buněk přidáním omezení – vyberte změny buněk, které chcete použít, a pak v seznamu v dialogovém okně Přidat omezení zvolte Přihrádka.

S tímto pozadím jsme připraveni vyřešit problém výběru softwarového projektu. Jako vždy u modelu Řešitele začneme tím, že identifikujeme cílovou buňku, měnící se buňky a omezení.

• Cílová buňka. Maximalizujeme hodnoty NPV vygenerované vybranými projekty.

• Změna buněk. Pro každý projekt hledáme binární buňku s 0 nebo 1. Tyto buňky jsem vyhlašoval(a) v oblasti A6:A25 (a pojmenoval oblast doit). Například číslo 1 v buňce A6 označuje, že provádíme Projekt 1; Hodnota 0 v buňce C6 značí, že nespustíme projekt 1.

• Omezení. Musíme zajistit, aby pro každý rok t (t=1, 2, 3) byl použitý kapitál menší než nebo roven roku t kapitálu k dispozici a rok t využité práce je menší nebo roven roku t práce k dispozici.

Jak vidíte, náš list musí vypočítat pro jakýkoli výběr projektů NPV, každoročně využitý kapitál a programátoři používaná každý rok. V buňce B2 používám vzorec SUMPRODUCT(doit;NPV) k výpočtu celkového počtu npv vygenerovaných vybranými projekty. (Název oblasti NPV odkazuje na oblast C6:C25.) Pro každý projekt s 1 ve sloupci A tento vzorec přebírá hodnotu NPV projektu a pro každý projekt s 0 ve sloupci A tento vzorec nepřebírá hodnotu NPV projektu. Proto jsme schopni vypočítat hodnotu NPV všech projektů a naše cílová buňka je lineární, protože se počítá součtem termínů, které následují za tvarem (změna buňky)*(konstanty). Podobným způsobem vypočítám každý rok použitý kapitál a ročně využitou práci zkopírováním vzorce SUMPRODUCT(doit,E6:E25) z E2 do F2:J2.

Teď vyplňuji dialogové okno Parametry Řešitele, jak je znázorněno na obrázku 30-2.

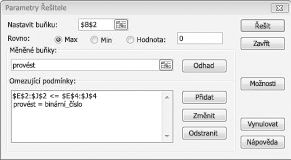
Naším cílem je maximalizovat hodnotu NPV vybraných projektů (buňka B2). Naše měnící se buňky (oblast s názvem doit) jsou binární buňky pro každý projekt. Omezení E2:J2<=E4:J4 zajišťuje, že během každého roku bude využitý kapitál a práce menší nebo roven kapitálu a práci k dispozici. Chcete-li přidat omezení, které změní buňky binární, klikněte na tlačítko Přidat v dialogovém okně Parametry řešitele a pak vyberte možnost Přihrádka ze seznamu uprostřed dialogového okna. Dialogové okno Přidat omezení by se mělo zobrazit jako na obrázku 30-3.

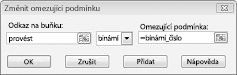
Náš model je lineární, protože cílová buňka se vypočítá jako součet termínů, které mají tvar (změna buňky)*(konstanty), a protože omezení využití prostředků se počítají porovnáním součtu (měnících se buněk)*(konstant) s konstantou.

Po vyplnění dialogového okna Parametry řešitele klikněte na Vyřešit a výsledky jsou zobrazené dříve na obrázku 30-1. Společnost může získat maximální hodnotu NPV ve výši 9 293 milionů USD (9,293 miliardy USD) volbou projektů 2, 3, 6–10, 14–16, 19 a 20.

Někdy mají modely výběru projektů jiná omezení. Předpokládejme například, že když vybereme Project 3, musíme vybrat také Project 4. Vzhledem k tomu, že naše aktuální optimální řešení vybírá Project 3, ale ne Project 4, víme, že naše aktuální řešení nemůže zůstat optimální. Chcete-li tento problém vyřešit, jednoduše přidejte omezení, že binární změna buňky pro Project 3 je menší než nebo roven binární měněné buňce aplikace Project 4.

Tento příklad najdete na listu Pokud 3 pak 4 v souboru Capbudget.xlsx, který je znázorněn na obrázku 30-4. Buňka L9 odkazuje na binární hodnotu související s projektem 3 a buňku L12 na binární hodnotu související s aplikací Project 4. Když přidáme omezení L9<=L12, pokud zvolíme Project 3, L9 se rovná 1 a naše omezení vynutí L12 (binární soubor Projektu 4) na hodnotu 1. Pokud nevybereme Project 3, musí naše omezení ponechat binární hodnotu v měněné buňce aplikace Project 4 bez omezení. Pokud nevybereme Project 3, hodnota L9 se rovná 0 a naše omezení umožní binárnímu souboru aplikace Project 4, aby se rovnal hodnotě 0 nebo 1, což je to, co chceme. Nové optimální řešení je znázorněno na obrázku 30-4.

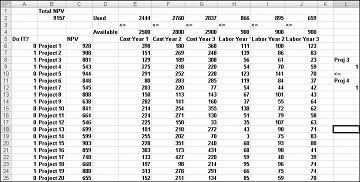
Nové optimální řešení se vypočítá, pokud výběr Projectu 3 znamená, že musíme vybrat také Projekt 4. Teď předpokládejme, že z projektů 1 až 10 můžeme provádět pouze čtyři projekty. (Viz list Maximálně 4 z P1–P10 na obrázku 30-5.) V buňce L8 vypočítáme součet binárních hodnot přidružených k projektům 1 až 10 pomocí vzorce SUMA(A6:A15). Pak přidáme omezení L8<=L10, což zajistí, že budou vybrány maximálně 4 z prvních 10 projektů. Nové optimální řešení je znázorněno na obrázku 30-5. Čistá hodnota se snížila na 9,014 miliardy dolarů.

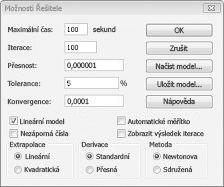
Modely lineárního řešitele, ve kterých některé nebo všechny měnící se buňky musí být binární nebo celočíselné, jsou obvykle obtížnější než lineární modely, ve kterých mohou být všechny měnící se buňky zlomky. Z tohoto důvodu jsme často spokojení s téměř optimálním řešením problému binárního nebo celočíselného programování. Pokud model Řešitele běží dlouhou dobu, můžete zvážit úpravu nastavení tolerance v dialogovém okně Možnosti řešitele. (Viz obrázek 30-6.) Například nastavení tolerance 0,5 % znamená, že Řešitel se zastaví, když poprvé najde proveditelné řešení, které je v rozmezí 0,5 % teoreticky optimální cílové hodnoty buňky (teoretická optimální cílová hodnota je optimální cílová hodnota nalezená při vynechání binárních a celočíselných omezení). Často stojíme před volbou mezi nalezením odpovědi do 10 procent optimálního za 10 minut nebo nalezením optimálního řešení za dva týdny počítačového času. Výchozí hodnota tolerance je 0,05 %, což znamená, že Řešitel se zastaví, když najde hodnotu cílové buňky v rozmezí 0,05 % teoreticky optimální cílové hodnoty buňky.

1. Společnost uvažuje o devíti projektech. V následující tabulce je uvedena hodnota NPV přidaná každým projektem a kapitál vyžadovaný jednotlivými projekty během následujících dvou let. (Všechna čísla jsou v milionech.) Například Project 1 přidá 14 milionů USD na hodnotu čistá virtuální zařízení a vyžaduje výdaje ve výši 12 milionů USD během roku 1 a 3 miliony usd během roku 2. Během 1. roku je pro projekty k dispozici 50 milionů usd kapitálu a 20 milionů usd během roku 2.

	NPV	Výdaje za rok 1	Rok 2 výdaje
Project 1	14	12	3
Project 2	17	54	7
Project 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
Project 6	12	6	6
Project 7	14	48	4
Project 8	10	36	3
Project 9	12	18	3

• Pokud nemůžeme provést zlomek projektu, ale musíme provést buď celý projekt, nebo žádný z nich, jak můžeme maximalizovat výkonnou hodnotu?

• Předpokládejme, že pokud se projekt 4 provádí, musí být proveden Projekt 5. Jak můžeme maximalizovat funkci NPV?

• Vydavatelská společnost se snaží určit, kterou z 36 knih by měla vydat letos. Soubor Pressdata.xlsx poskytuje následující informace o každé knize:

  • Předpokládané výnosy a náklady na vývoj (v tisících dolarů)

  • Stránky v každé knize

  • Zda je kniha zaměřená na cílovou skupinu vývojářů softwaru (označená 1 ve sloupci E)

    Vydavatelská společnost může letos publikovat knihy o celkovém počtu až 8500 stran a musí publikovat alespoň čtyři knihy zaměřené na vývojáře softwaru. Jak může společnost maximalizovat svůj zisk?

Tento článek byl upraven z aplikace Microsoft Office Excel 2007 Data Analysis and Business Modeling od Wayna L. Winstona.

Tato učebnická kniha byla vyvinuta ze série prezentací Wayna Winstona, známého statistika a obchodního profesora, který se specializuje na kreativní a praktické aplikace Excelu.