В тази статия е описан синтаксисът и употребата на функцията ZTEST в Microsoft Excel.
Връща едностранната стойност на вероятност на z-тест. За дадена средна генерална съвкупност с хипотеза, μ0, ZTEST връща вероятността средната стойност да бъде по-голяма от средната стойност на наблюденията в набора данни (масив) – т.е. наблюдаваната средна стойност.
За да видите как ZTEST може да се използва във формула за пресмятане на двустранна вероятностна стойност, вижте "Забележки" по-долу.
Важно: Тази функция е заместена с една или няколко нови функции, които могат да предоставят подобрена точност и чиито имена по-добре отразяват употребата им. Макар че тази функция все още е достъпна за обратна съвместимост, трябва да обмислите използването на новите функции от сега нататък, защото тази функция може да не е достъпна в бъдещи версии на Excel.
За повече информация относно новата функция вж. Z.TEST функция.
Синтаксис
ZTEST(масив;x;[сигма])
Синтаксисът на функцията ZTEST има следните аргументи:
-
"масив" Задължително. Масив или диапазон от данни, за който да се провери x.
-
X Задължително. Стойността, която се проверява.
-
"сигма" Незадължително. Стандартното отклонение на генералната съвкупност (известната). Ако се пропусне, се използва стандартното отклонение на извадка.
Забележки
-
Ако масив е празно, ZTEST връща грешната стойност #N/A.
-
Когато сигма не е пропуснато, ZTEST се пресмята както следва:
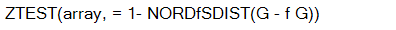
или когато сигма е пропуснато:
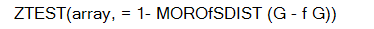
където x е средната стойност AVERAGE(масив); s е стандартното отклонение на извадката STDEV(масив); а n е броят на наблюдения в извадката COUNT(масив).
-
ZTEST представлява вероятността средната стойност да е по-голяма от наблюдаваната стойност AVERAGE(масив), когато средната стойност на генералната съвкупност е μ0. От симетрията на нормалното разпределение, ако AVERAGE(масив) < μ0, ZTEST ще върне стойност, по-голяма от 0.5.
-
Следващата формула на Excel може да се използва за пресмятане на двустранната вероятност средната стойност да бъде по-далече от μ0 (във всяка посока), отколкото AVERAGE(масив), когато средната стойност на генералната съвкупност е μ0:
=2 * MIN(ZTEST(масив;μ0;сигма), 1 – ZTEST(масив;μ0;сигма)).
Пример
Копирайте примерните данни в следващата таблица и ги поставете в клетка A1 на нов работен лист на Excel. За да покажат резултати формулите, изберете ги, натиснете клавиша F2 и след това натиснете клавиша Enter. Ако е необходимо, коригирайте ширините на колоните, за да видите всичките данни.
|
Данни |
||
|
3 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
6 |
||
|
5 |
||
|
4 |
||
|
2 |
||
|
1 |
||
|
9 |
||
|
Формула |
Описание (Резултат) |
Резултат |
|
=ZTEST(A2:A11;4) |
Стойност на едностранно ограничена вероятност на z-тест за набора данни по-горе при средната генерална съвкупност с направена хипотеза от 4 (0,090574) |
0,090574 |
|
=2 * MIN(ZTEST(A2:A11;4); 1 - ZTEST(A2:A11;4)) |
Стойност на двустранно ограничена вероятност на z-тест за набора данни по-горе при средната генерална съвкупност с направена хипотеза от 4 (0,181148) |
0,181148 |
|
=ZTEST(A2:A11;6) |
Стойност на едностранно ограничена вероятност на z-тест за набора данни по-горе при средната генерална съвкупност с направена хипотеза от 6 (0,863043) |
0,863043 |
|
=2 * MIN(ZTEST(A2:A11;6); 1 - ZTEST(A2:A11;6)) |
Стойност на двустранно ограничена вероятност на z-тест за набора данни по-горе при средната генерална съвкупност с направена хипотеза от 6 (0,273913) |
0,273913 |










