Забележка: Бихме искали да ви осигурим най-новото помощно съдържание възможно най-бързо на вашия собствен език. Тази страница е преведена чрез автоматизация и може да съдържа граматически грешки и несъответствия. Нашата цел е това съдържание да ви бъде полезно. Можете ли да ни кажете дали информацията е била полезна за вас, в дъното на тази страница? Ето статията на английски за бърза справка.
Изчислява нетната настояща стойност на инвестиция с помощта на дисконтова ставка и последователност от бъдещи плащания (отрицателни стойности) и приходи (положителни стойности).
Синтаксис
NPV(rate,value1,value2,...)
Rate е дисконтовата ставка върху един период.
Value1, value2,... за от 1 до 29 на брой аргумента, представляващи плащанията и приходите. Value1, value2,... трябва да бъдат периодично разпределени във времето и възникват в края на всеки период. NPV използва реда на value1, value2,... за да интерпретира реда в потока на средствата. Уверете се, че сте въвели плащанията и постъпленията в правилната им последователност. Зачитат се аргументите, които са числа, логически стойности, текстови представяния на числа или са празни; аргументите, които са стойности на грешки или текст, който не може да бъде конвертиран в числа, се игнорират.
Забележки
-
NPV инвестицията започва един период преди датата на паричния поток стойност1 и завършва с последния паричен поток в списъка. Изчислението на NPV е на базата на бъдещи парични потоци. Ако вашият първи паричен поток е в началото на първия период, първата стойност трябва да се добави към резултата от NPV, който не е включен в аргументите. За повече информация вж. примерите по-долу.
-
Ако n е броят на паричните потоци в списъка от стойности, формулата за NPV е:
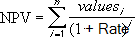
-
NPV е подобна на функцията PV (настояща стойност). Основната разлика между PV и NPV е това, че PV позволява паричните потоци да започват или в края, или в началото на периода. За разлика от променливите стойности на паричните потоци в NPV, при PV паричните потоци по време на инвестицията трябва да са постоянни. За информация за анюитетните и финансовите функции вж. PV.
Пример 1
В този пример:
-
Rate e годишната дисконтова ставка.
-
Value1 е първоначалния разход за инвестиция за една година от днес.
-
Value2 е възвръщаемостта от първата година.
-
Value3 е възвръщаемостта през втората година.
-
Value4 е възвръщаемостта за третата година.
В примера трябва да включите първоначалните $10 000 като една от стойностите, защото плащането се извършва в края на първия период.
|
Rate |
Value1 |
Value2 |
Value3 |
Value4 |
Формула |
Описание (Резултат) |
|
10% |
-10000 |
3000 |
4200 |
6800 |
=NPV([Rate], [Value1], [Value2], [Value3], [Value4]) |
Нетна настояща стойност на тази инвестиция (1188,44) |
Пример 2
В този пример:
-
Rate e годишната дисконтова ставка. Това може да представлява процента на инфлацията или лихвения процент на конкурентна инвестиция.
-
Value1 е първоначалния разход за инвестиция за една година от днес.
-
Value2 е възвръщаемостта от първата година.
-
Value3 е възвръщаемостта през втората година.
-
Value4 е възвръщаемостта през третата година.
-
Value5 е възвръщаемостта през четвъртата година.
-
Value6 е възвръщаемостта за петата година.
В примера не трябва да включвате първоначалните $40 000 като една от стойностите, защото плащането се извършва в началото на първия период.
|
Rate |
Value1 |
Value2 |
Value3 |
Value4 |
Value5 |
Value6 |
Формула |
Описание (Резултат) |
|
8% |
-40000 |
8000 |
9200 |
10000 |
12000 |
14500 |
=NPV(Rate, [Value2], [Value3], [Value4], [Value5], [Value6])+[Value1] |
Нетна настояща стойност на тази инвестиция (1 992,06) |
|
8% |
-40000 |
8000 |
9200 |
10000 |
12000 |
14500 |
=NPV(Rate, [Value2], [Value3], [Value4], [Value5], [Value6], -9000)+[Value1] |
Настояща нетна стойност на тази инвестиция със загуба през шестата година (-3749,47) |










