Използване на Analysis ToolPak за извършване на сложен анализ на данни

1. Щракнете върху раздела Файл, щракнете върху Опции, а след това щракнете върху категорията Добавки.

2. В полето Управление изберете Добавки на Excel, а след това щракнете върху Почни.

   Ако използвате Excel for Mac, в менюто "Файл" отидете на Инструменти > Добавки за Excel.

3. В полето Добавки отметнете квадратчето Analysis ToolPak и след това щракнете върху OK.

   • Ако Analysis ToolPak не е показан в полето Налични добавки, щракнете върху Преглед, за да го откриете.

   • Ако се появи подсещащо съобщение за това, че Analysis ToolPak не е инсталиран на компютъра ви, щракнете върху Да, за да го инсталирате.

Инструментите за анализ на Anova предоставят различни типове дисперсионен анализ. Инструментът, който трябва да използвате, зависи от броя на факторите и от броя на образците (извадките), които имате от генералните съвкупности, които искате да проверите.

Anova: Еднофакторен

Този инструмент извършва прост анализ на дисперсията на данните за две или повече извайки. Анализът предоставя тест на хипотезата, че всяка извадка се извлича от едно и също основно вероятностно разпределение спрямо алтернативната хипотеза, че базовите вероятностни разпределения не са едни и същи за всички извадки. Ако има само два примера, можете да използвате функцията за работен лист T."ТЕСТ". С повече от две проби няма удобно обобщаване на Т.ВМЕСТО това може да бъде извикан моделът "Единичен фактор Анова".

Anova: Двуфакторен с репликация

Този инструмент за анализ е полезен, когато данните могат да се класифицират по две различни измерения. Например в един експеримент за измерване на височината на растения, на растенията могат да са предоставени различни видове тор (например A, B, C) и може също така да се пазят при различни температури (например ниска и висока). За всяка от шестте възможни двойки {тор, температура} имаме еднакъв брой наблюдения за височината на растенията. Използвайки този инструмент на Anova, можем да проверим:

• Дали височините на растенията за различните марки торове се получават от една и съща основна генерална съвкупност. При този анализ температурите се игнорират.

• Дали височините на растенията за различните температури се извличат от една и съща основна генерална съвкупност. Видовете торове се игнорират за този анализ.

Дали се отчитат последиците от разликите в марките тор, намерени в първата точка, и от различните температури, намерени във втората точка, шестте извадки, представящи всички двойки {тор, температура}, са изтеглени от една и съща генерална съвкупност. Алтернативната хипотеза е, че има последици, които се дължат на спецификата на двойките {тор, температура}, надхвърлящи разликите, базиращи се на въздействията на вида тор и температурата, взети поотделно.

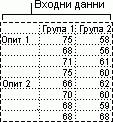
Anova: Двуфакторен без репликация

Този инструмент за анализ е полезен, когато данните са класифицирани по две различни размерности като двуфакторния случай с репликация. Обаче за този инструмент се приема, че има само единични наблюдения за всяка двойка (например всяка двойка {тор, температура} в предишния пример).

Функциите за работен лист CORREL и PEARSON изчисляват коефициента на корелация между две променливи на измерване, когато измерванията на всяка променлива се наблюдават за всеки от N обектите. (Всяко липсващо наблюдение по някаква тема кара този обект да бъде игнориран в анализа.) Инструментът за анализ на корелация е особено полезен, когато има повече от две променливи на измерване за всеки от N обектите. Предоставя изходна таблица – матрица на корелация, която показва стойността на CORREL (или PEARSON), приложена към всяка възможна двойка променливи на измерване.

Коефициентът на корелация, подобно на ковариацията, е мярка за степента, в която две променливи на измерване "се променят заедно". За разлика от ковариацията коефициентът на корелация се мащабира така, че стойността му е независима от единиците, в които са изразени двете променливи на измерване. (Ако например двете променливи на измерване са тегло и височина, стойността на коефициента на корелация се променя, ако теглото се преобразува от килограми в килограми.) Стойността на всеки коефициент на корелация трябва да бъде между -1 и +1 включително.

Можете да използвате инструмента за корелационен анализ, за да изследвате всяка двойка променливи на измервания, за да определите дали двете променливи на измервания имат тенденция да се променят едновременно – тоест дали големите стойности на едната променлива имат склонност да са свързани с големи стойности на другата (положителна корелация), или малките стойности на едната променлива имат склонност да са свързани с големи стойности на другата (отрицателна корелация) и дали стойностите на двете променливи имат склонност да не са свързани (корелация, близка до 0 (нула)).

И двата инструмента за корелация и ковариация могат да се използват с еднаква настройка, когато имате N различни променливи на измервания, наблюдавани за набор от индивиди. Всеки един от инструментите за корелация и ковариация дава изходна таблица – една матрица, която показва съответно коефициента на корелация или ковариация, между всяка двойка променливи на измерване. Разликата е в това, че коефициентите на корелация са мащабирани да лежат в интервала между -1 и +1, включително. Съответните ковариации не са мащабирани. И коефициентът на корелация, и коефициентът на ковариация са мерки на степента, в която две променливи "се променят съвместно".

Инструментът за ковариация изчислява стойността на функцията за работен лист COVARIANCE. P за всяка двойка променливи на измерване. (Директно използване на COVARIANCE. P, а не инструментът за ковариация, е разумна алтернатива, когато има само две променливи на измерване, т.е. N=2.) Записът в диагонала на изходната таблица на инструмента за ковариация в ред i, колона i е ковариацията на i-тата променлива на измерване със себе си. Това е само дисперсията на генералната съвкупност за тази променлива, изчислена от функцията VAR на работния лист.P. P.

Можете да използвате инструмента за ковариация, за да изследвате всяка двойка променливи на измервания, за да определите дали двете променливи на измервания имат тенденция да се променят едновременно – тоест дали големите стойности на едната променлива имат склонност да са свързани с големи стойности на другата (положителна ковариация), или малките стойности на едната променлива имат склонност да са свързани с големи стойности на другата (отрицателна ковариация) и дали стойностите на двете променливи имат склонност да не са свързани (ковариация, близка до 0 (нула)).

Инструментът за анализ на описателни статистики генерира отчет на едновременно променящи се статистики за данни във входния диапазон, предоставяйки информация за основната тенденция на вашите данни.

Инструментът за анализ на експоненциално изглаждане предсказва стойност, която е базирана на прогнозата за предишния период, регулирана за грешката в тази предишна прогноза. Инструментът използва константата на изглаждане a, големината на която определя колко точно прогнозите отговарят на грешката в по-раншната прогноза.

Инструментът за F-тест на две извадки за дисперсии извършва F-тест за две извадки, за да сравни две дисперсии на генерални съвкупности.

Например можете да използвате инструмента за F-тест за образци на времена в състезание по плуване за два отбора. Инструментът предоставя резултата от тест при нулевата хипотеза, че тези две извадки произхождат от разпределения с равни дисперсии, срещу алтернативата, че дисперсиите не са равни в подразбиращите се разпределения.

Инструментът изчислява стойността f на F-статистика (или F-пропорция). Стойност на f, близка до 1, предоставя доказателство на факта, че подразбиращите се дисперсии са равни. В изходната таблица, ако f < 1 "P(F <= f) едностранно" дава вероятността за наблюдаване на стойност на F-статистиката, която да е по-малка от f, когато дисперсиите на генералните съвкупности са равни, а "F критично едностранно" дава критичната стойност, по-малка от 1, за избраното ниво на значимост алфа. Ако f > 1, "P(F <= f) едностранно" дава вероятността за наблюдаване на стойност на F-статистиката, по-голяма от f, когато дисперсиите на генералната съвкупност са равни, а "F критично едностранно" дава критичната стойност, по-голяма от 1, за алфа.

Инструментът за Фурие анализ решава проблеми в линейни системи и анализира периодични данни с помощта метода на бързото преобразование на Фурие (FFT) за преобразуване на данни. Този инструмент поддържа също обратни преобразувания, в които обратните на преобразуваните данни отговарят на първоначалните данни.

Инструментът за анализ на хистограми изчислява отделни и кумулативни честоти за диапазон от клетки за данни и обединения. Този инструмент генерира данни за броя на повторенията на стойност в набор от данни.

Например в клас от 20 студенти можете да определите разпределението на точките в побуквено класирани категории. Таблицата на хистограмата представя побуквено класираните граници и броя на точките между най-ниската граница и текущата граница. Единственият най-често срещан брой точки е модата на данните.

Инструментът за анализ на подвижна средна стойност планира стойности в прогнозния период, базирани на средната стойност на променливата за определен брой предшестващи периоди. Подвижната средна стойност предоставя информация за тенденцията, която простата средна стойност на всички хронологични данни би маскирала. Използвайте този инструмент, за да прогнозиране на продажби, запаси или други тенденции. Всяка прогнозна стойност се базира на следната формула.

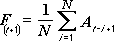
където:

• N е броят на предишните периоди, които да се включат в подвижната средна стойност

• A j е действителната стойност в момента j

• F j е прогнозираната стойност за момента j

Инструментът за анализ на генериране на случайни числа попълва диапазон с независими случайни числа, които се изтеглят от едно или няколко разпределения. Можете да характеризирате обектите в генералната съвкупност заедно с разпределение на вероятностите. Например можете да използвате нормално разпределение, за да характеризирате генералната съвкупност от височини на индивиди или пък можете да използвате разпределение на Бернули за два възможни изхода, за да характеризирате генералната съвкупност на резултати от хвърляне на монета.

Инструментът за ранг и процентил анализ създава таблица, която съдържа подреждането и ранга в проценти на всяка стойност в набор данни. Можете да анализирате относителното положение на стойностите в набор данни. Този инструмент използва функциите за работен лист RANK. EQ иPERCENTRANK. InC. Ако искате да се вземат предвид свързаните стойности, използвайте RANK. Функцията EQ , която третира свързаните стойности като имащи един и същ ранг, или използва RANK.Функция AVG , която връща средния ранг на свързаните стойности.

Инструментът за регресионен анализ извършва линеен регресионен анализ с помощта на метода на "най-малките квадрати", за да нагоди линия през набор от наблюдения. Можете да анализирате как единична зависима променлива се влияе от стойностите на една или няколко независими променливи. Например можете да анализирате как се влияят постиженията на спортистите от такива фактори като възраст, височина и тегло. Можете да разпределите дялове в измерването на постижението за всеки от тези фактори, базирани на данните за постижението, а след това да използвате резултатите, за да предскажете постижението на нов, неизпробван спортист.

Инструментът за регресия използва функцията за работен лист LINEST.

Инструментът за анализ на изтегляне на извадка създава извадка от генерална съвкупност чрез третирането на входния диапазон като генерална съвкупност. Когато генералната съвкупност е твърде голяма за обработка или начертаване, можете да използвате представителна извадка. Можете също да създадете извадка, която съдържа само стойностите от конкретна част на серия, ако предполагате, че входните данни са периодични. Например ако входният диапазон съдържа суми за тримесечни продажби, периодичното изтегляне на извадки с период четири поставя стойностите от едно и също тримесечие в изходната таблица.

Инструментите за анализ на t-тест с две извадки тестват за равенство на средни стойности на генералните съвкупности, които са в основата на всяка извадка. Трите инструмента използват различни допускания: че дисперсиите на генералните съвкупности са равни, че дисперсиите на генералните съвкупности не са равни и че двете извадки представляват наблюдения преди и след обработката на едни и същи обекти.

За всичките три инструмента по-долу стойността на t-статистиката t се пресмята и показва като "t Stat" в изходните таблици. В зависимост от данните тази стойност t може да бъде отрицателна или неотрицателна. При предположение за равенство на средните стойности на стоящите в основата генерални съвкупности, ако t < 0, "P(T <= t) едностранно" дава вероятността, че стойността на t-статистиката би била наблюдавана като по-отрицателна от t. Ако t >=0, "P(T <= t) едностранно" дава вероятността стойността на t-статистиката да се наблюдава като по-положителна от t. "t критично едностранно" дава отрязаната стойност, така че вероятността за наблюдаване на стойността на t-статистиката да е по-голяма или равна от "t критично едностранно" е алфа.

"P(T <= t) двустранно" дава вероятността, че стойността на t-статистиката би била наблюдавана като по-голяма по абсолютна стойност от t. "P критично двустранно" дава отрязаната стойност, така че вероятността t-статистиката да бъде наблюдавана като по-голяма по абсолютна стойност от "P критично двустранно" е алфа.

t-тест: Две сдвоени по средни стойности извадки

Можете да използвате сдвоен тест, когато има естествено сдвояване на наблюдения в извадки, като например когато група извадки се изпитва два пъти – преди и след експеримента. Този инструмент за анализ и неговата формула, извършват сдвоен t-тест на Стюдънт за две извадки, за да определят дали наблюденията, които са извършени преди обработката, и наблюденията, които са извършени след обработката, е вероятно да произлизат от разпределения с еднакви средни стойности на генералната съвкупност. Тази форма на t-теста не предполага, че дисперсиите на двете генерални съвкупности са равни.

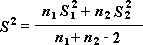
t-тест: Две извадки с предполагаемо равни дисперсии

Този инструмент за анализ извършва t-тест на Стюдънт с две извадки. Тази форма на t-тест предполага, че двата набора данни се получават от разпределения с еднакви дисперсии. Той се посочва като t-тест с еднаква дисперсия. Можете да използвате този t-тест, за да определите дали е вероятно две извадки да произхождат от разпределения с равни средни стойности на генералната съвкупност.

t-тест: Две извадки с предполагаемо неравни дисперсии

Този инструмент за анализ извършва t-тест на Стюдънт с две извадки. Тази форма на t-тест предполага, че двата набора данни се получават от разпределения с неравни дисперсии. Той се посочва като t-тест с различна дисперсия. Както в предишния случай на равни дисперсии, можете да използвате този t-тест, за да определите дали е вероятно две извадки да произхождат от разпределения с равни средни стойности на генералната съвкупност. Използвайте този тест, когато в двете извадки има различни обекти. Използвайте сдвоения тест, описан в следващия пример, когато има единичен набор от обекти и двете извадки представят измервания за всеки обект – преди и след обработка.

Следната формула се използва за определяне на стойността на статистиката t.

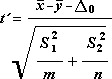
Следната формула се използва за изчисляване на степените на свобода, df. Тъй като резултатът от изчислението обикновено не е цяло число, стойността на df се закръглява до най-близкото цяло число, за да се получи критична стойност от t таблицата. Функцията за работен лист на Excel T.TEST използва изчислената стойност на df без закръгляване, защото е възможно да се изчисли стойност за T.TEST с неинтехниално df. Поради тези различни подходи за определяне на степените на свобода резултатите от T.TEST и този инструмент за t-тест ще се различават в случая с Unequal Variances.

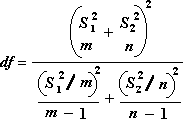
Z-тестът: Две извадки за инструмента за анализ на средства извършват две извадки от z-тест за средства с известни дисперсии. Този инструмент се използва за проверка на нулевата хипотеза, че няма разлика между две средства на генералната съвкупност спрямо едностранни или двустранни алтернативни хипотези. Ако дисперсиите не са известни, функцията за работен лист Z.Вместо това трябва да се използва ТЕСТ.

Когато използвате инструмента за z-тест, бъдете внимателни, за да разберете резултата. "P(Z <= z) едностранно" е всъщност P(Z >= ABS(z)) – вероятността z-стойност да бъде по-далеч от 0 в същата посока като наблюдаваната z стойност, когато няма разлика между средните стойности на генералните съвкупности. "P(Z <= z) двустранно" е всъщност P(Z >= ABS(z) или Z <= -ABS(z)) – вероятността на z-стойността да е по-далеч от 0 от наблюдаваната z-стойност, в едната или другата посока, когато няма разлика между средните стойности на генералните съвкупности. Двустранният резултат е точно едностранният резултат, умножен по 2. Инструментът за z-тест може също така да се използва за случая, когато нулевата хипотеза е, че има конкретна ненулева стойност за разликата между двете средни стойности на генералните съвкупности. Например можете да използвате този тест, за да определите разликите в експлоатационните качества на два модела коли.