استخدام Solver لموازنة رأس المال

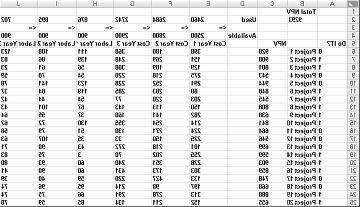
وترغب معظم الشركات في الاضطلاع بمشاريع تساهم في تحقيق أكبر قيمة صافية للقيمة الحالية، رهنا بموارد محدودة (عادة ما تكون رأس المال والعمالة). لنفترض أن شركة تطوير البرمجيات تحاول تحديد أي من 20 مشروعا برمجيا يجب أن تقوم بها. يتم تقديم الدالة NPV (بملايين الدولارات) التي يساهم بها كل مشروع وكذلك رأس المال (بملايين الدولارات) وعدد المبرمجين المطلوبين خلال كل سنة من السنوات الثلاث القادمة في ورقة عمل النموذج الأساسي في ملف Capbudget.xlsx، الذي يظهر في الشكل 30-1 في الصفحة التالية. على سبيل المثال، ينتج عن Project 2 908 مليون دولار. وهي تتطلب 151 مليون دولار خلال السنة 1، و 269 مليون دولار خلال السنة الثانية، و 248 مليون دولار خلال السنة 3. يتطلب المشروع 2 139 مبرمجا خلال السنة 1، و86 مبرمجا خلال السنة الثانية، و83 مبرمجا خلال السنة الثالثة. تعرض الخلايا E4:G4 رأس المال (بملايين الدولارات) المتوفرة خلال كل سنة من السنوات الثلاث، وتشير الخلايا H4:J4 إلى عدد المبرمجين المتاحين. فعلى سبيل المثال، خلال السنة 1، يتوفر ما يصل إلى 2.5 بليون دولار من رأس المال و 900 مبرمج.

يجب أن تقرر الشركة ما إذا كان يجب أن تقوم بكل مشروع. لنفترض أنه لا يمكننا الاضطلاع بجزء صغير من مشروع البرامج؛ إذا خصصنا 0.5 من الموارد المطلوبة، على سبيل المثال، سيكون لدينا برنامج غير عملي من شأنه أن يحقق لنا إيرادات 0 دولار!

الخدعة في حالات النمذجة التي تقوم فيها أو لا تفعل شيئا ما هي استخدام الخلايا المتغيرة الثنائية. دائما ما تساوي الخلية الثنائية المتغيرة 0 أو 1. عندما تساوي الخلية المتغيرة الثنائية التي تتوافق مع مشروع ما 1، نقوم بالمشروع. إذا كانت الخلية الثنائية المتغيرة التي تتوافق مع مشروع تساوي 0، فلن نقوم بالمشروع. يمكنك إعداد Solver لاستخدام نطاق من الخلايا الثنائية المتغيرة عن طريق إضافة قيد — حدد الخلايا المتغيرة التي تريد استخدامها ثم اختر سلة من القائمة في مربع الحوار إضافة قيد.

باستخدام هذه الخلفية، نحن مستعدون لحل مشكلة تحديد مشروع البرنامج. كما هو الحال دائما مع نموذج Solver، نبدأ بتحديد الخلية المستهدفة والخلايا المتغيرة والقيود.

• الخلية الهدف. نقوم بتكبير NPV الذي تم إنشاؤه بواسطة مشاريع محددة.

• تغيير الخلايا. نحن نبحث عن خلية ثنائية متغيرة 0 أو 1 لكل مشروع. لقد حددت موقع هذه الخلايا في النطاق A6:A25 (وقمت بتسمية النطاق doit). على سبيل المثال، يشير 1 في الخلية A6 إلى أننا نضطلع بالمشروع 1؛ يشير 0 في الخلية C6 إلى أننا لا نقوم بتنفيذ Project 1.

• القيود. نحن بحاجة إلى التأكد من أنه لكل سنة t (t=1، 2، 3)، رأس مال السنة t المستخدم أقل من أو يساوي رأس المال T السنة المتوفرة، والعمالة السنوية المستخدمة أقل من أو تساوي السنة t العمالة المتاحة.

كما ترى، يجب أن يتم حساب ورقة العمل الخاصة بنا لأي مجموعة من المشاريع التي يستخدمها NPV، ورأس المال المستخدم سنويا، والمبرمجون المستخدمون كل عام. في الخلية B2، أستخدم الصيغة SUMPRODUCT(doit,NPV) لحساب إجمالي NPV الذي تم إنشاؤه بواسطة مشاريع محددة. (يشير اسم النطاق NPV إلى النطاق C6:C25.) لكل مشروع مع 1 في العمود A، تلتقط هذه الصيغة NPV للمشروع، ولكل مشروع يحتوي على 0 في العمود A، لا تلتقط هذه الصيغة NPV للمشروع. لذلك، يمكننا حساب NPV لجميع المشاريع، والخلية المستهدفة خطية لأنه يتم حسابها عن طريق جمع المصطلحات التي تتبع النموذج (تغيير الخلية)*(ثابت). بطريقة مماثلة، أحسب رأس المال المستخدم كل عام والعمالة المستخدمة كل عام عن طريق نسخ من E2 إلى F2:J2 الصيغة SUMPRODUCT(doit,E6:E25).

أملأ الآن مربع الحوار Solver Parameters كما هو موضح في الشكل 30-2.

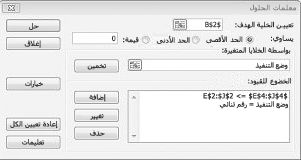
هدفنا هو زيادة NPV للمشاريع المحددة (الخلية B2). الخلايا المتغيرة (النطاق المسمى doit) هي الخلايا المتغيرة الثنائية لكل مشروع. يضمن القيد E2:J2<=E4:J4 أن رأس المال والعمالة المستخدمة أقل من أو يساوي رأس المال والعمالة المتاحة. لإضافة القيد الذي يجعل الخلايا المتغيرة ثنائية، انقر فوق إضافة في مربع الحوار معلمات Solver ثم حدد Bin من القائمة في منتصف مربع الحوار. يجب أن يظهر مربع الحوار إضافة قيد كما هو موضح في الشكل 30-3.

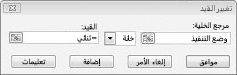
نموذجنا خطي لأنه يتم حساب الخلية الهدف كمجموع المصطلحات التي تحتوي على النموذج (خلية متغيرة)*(ثابت) ولأن قيود استخدام الموارد يتم حسابها عن طريق مقارنة مجموع (الخلايا المتغيرة)*(الثوابت) إلى ثابت.

مع ملء مربع الحوار معلمات Solver، انقر فوق حل ولدينا النتائج المعروضة سابقا في الشكل 30-1. يمكن للشركة الحصول على NPV بحد أقصى 9293 مليون دولار (9.293 مليار دولار) عن طريق اختيار المشاريع 2 و3 و6-10 و14-16 و19 و20.

في بعض الأحيان يكون لنماذج تحديد المشروع قيود أخرى. على سبيل المثال، افترض أنه إذا حددنا Project 3، فيجب علينا أيضا تحديد Project 4. نظرا لأن الحل الأمثل الحالي يحدد Project 3 وليس Project 4، فإننا نعلم أن الحل الحالي لا يمكن أن يظل الأمثل. لحل هذه المشكلة، ما عليك سوى إضافة القيد الذي يشير إلى أن الخلية المتغيرة الثنائية ل Project 3 أقل من الخلية المتغيرة الثنائية ل Project 4 أو مساوية لها.

يمكنك العثور على هذا المثال في ورقة العمل If 3 ثم 4 في الملف Capbudget.xlsx، والتي تظهر في الشكل 30-4. تشير الخلية L9 إلى القيمة الثنائية المتعلقة ب Project 3، والخلية L12 بالقيمة الثنائية المتعلقة ب Project 4. بإضافة القيد L9<=L12، إذا اخترنا Project 3، فإن L9 يساوي 1 ويجبر القيد L12 (الثنائي Project 4) على أن يساوي 1. يجب أن يترك قيدنا أيضا القيمة الثنائية في الخلية المتغيرة من Project 4 غير مقيد إذا لم نحدد Project 3. إذا لم نحدد Project 3، فإن L9 يساوي 0 ويسمح قيدنا لل ثنائي Project 4 بالتساوي بين 0 أو 1، وهو ما نريده. يظهر الحل الأمثل الجديد في الشكل 30-4.

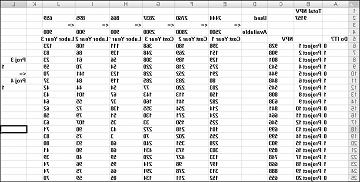
يتم حساب الحل الأمثل الجديد إذا كان تحديد Project 3 يعني أنه يجب علينا أيضا تحديد Project 4. الآن لنفترض أنه يمكننا القيام بأربعة مشاريع فقط من بين المشاريع من 1 إلى 10. (راجع ورقة العمل على الأكثر 4 من P1-P10 ، الموضحة في الشكل 30-5.) في الخلية L8، نحسب مجموع القيم الثنائية المقترنة ب Projects من 1 إلى 10 مع الصيغة SUM(A6:A15). ثم نضيف القيد L8<=L10، والذي يضمن، على الأكثر، تحديد 4 من أول 10 مشاريع. يظهر الحل الأمثل الجديد في الشكل 30-5. وانخفض الناتج القومي الإجمالي إلى 9.014 بليون دولار.

عادة ما يكون حل نماذج Solver الخطية التي تكون فيها بعض الخلايا المتغيرة أو جميعها ثنائية أو عدد صحيح أصعب من النماذج الخطية التي يسمح فيها بأن تكون جميع الخلايا المتغيرة كسور. لهذا السبب، غالبا ما نكون راضين عن حل شبه مثالي لمشكلة برمجة ثنائية أو عدد صحيح. إذا كان نموذج Solver يعمل لفترة طويلة، فقد تحتاج إلى التفكير في ضبط إعداد التسامح في مربع الحوار خيارات Solver. (راجع الشكل 30-6.) على سبيل المثال، يعني إعداد التسامح بنسبة 0.5٪ أن Solver سيتوقف في المرة الأولى التي يعثر فيها على حل ممكن يقع ضمن 0.5 بالمائة من قيمة الخلية الهدف المثلى النظرية (قيمة الخلية الهدف المثلى النظرية هي القيمة الهدف المثلى التي يتم العثور عليها عند حذف القيود الثنائية والعدد الصحيح). غالبا ما نواجه خيارا بين العثور على إجابة في غضون 10 بالمائة من المثلى في 10 دقائق أو العثور على الحل الأمثل في أسبوعين من وقت الكمبيوتر! قيمة التسامح الافتراضية هي 0.05٪، ما يعني أن Solver يتوقف عند العثور على قيمة خلية الهدف ضمن 0.05 بالمائة من قيمة الخلية الهدف المثلى النظرية.

1. شركة لديها تسعة مشاريع قيد النظر. يتم عرض القيمة NPV المضافة من قبل كل مشروع ورأس المال المطلوب من قبل كل مشروع خلال العامين القادمين في الجدول التالي. (جميع الأرقام بالملايين.) فعلى سبيل المثال، سيضيف المشروع 1 14 مليون دولار من النفقات المتوقعة ويتطلب نفقات تبلغ 12 مليون دولار خلال السنة 1 و 3 ملايين دولار خلال السنة الثانية. وخلال السنة 1، يتوفر رأس مال قدره 50 مليون دولار للمشاريع، ويتاح مبلغ 20 مليون دولار خلال السنة الثانية.

	NPV	نفقات السنة 1	نفقات السنة الثانية
المشروع 1	14	12	3
Project 2	17	54	7
المشروع 3	17	6	6
Project 4	15	6	2
Project 5	40	30	35
المشروع 6	12	6	6
Project 7	14	48	4
المشروع 8	10	36	3
Project 9	12	18	3

• إذا لم نتمكن من الاضطلاع بجزء صغير من المشروع ولكن يجب علينا القيام إما بكل مشروع أو لا شيء من المشروع، فكيف يمكننا زيادة NPV إلى أقصى حد؟

• لنفترض أنه إذا تم تنفيذ Project 4، فيجب تنفيذ Project 5. كيف يمكننا زيادة NPV إلى أقصى حد؟

• تحاول شركة نشر تحديد أي من الكتب ال 36 التي يجب نشرها هذا العام. يقدم Pressdata.xlsx الملف المعلومات التالية حول كل كتاب:

  • الإيرادات المتوقعة وتكاليف التنمية (بآلاف الدولارات)

  • صفحات في كل كتاب

  • ما إذا كان الكتاب موجها نحو جمهور من مطوري البرامج (المشار إليها بواسطة 1 في العمود E)

    يمكن لشركة نشر نشر نشر كتب يصل مجموعها إلى 8500 صفحة هذا العام ويجب أن تنشر أربعة كتب على الأقل موجهة لمطوري البرامج. كيف يمكن للشركة زيادة أرباحها إلى أقصى حد؟

تم تكييف هذه المقالة من Microsoft Office Excel 2007 Data Analysis and Business Modeling بواسطة واين ل. وينستون.

تم تطوير هذا الكتاب على غرار الفصل الدراسي من سلسلة من العروض التي قدمها واين وينستون، وهو إحصائي معروف وأستاذ أعمال متخصص في التطبيقات الإبداعية والعملية ل Excel.